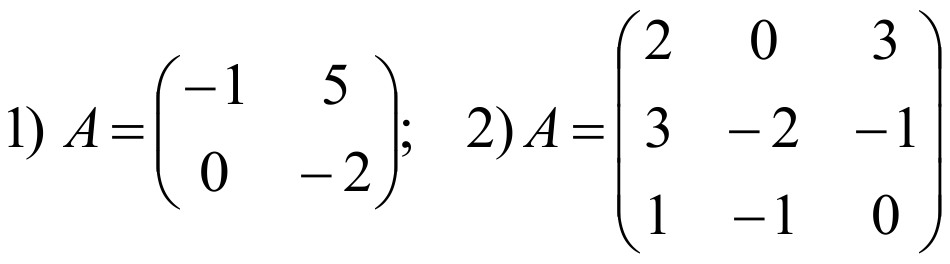
Обратная матрица

«Если Вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их.»
Д. Пойа (1887-1985 г.)

(Математик. Внёс большой вклад в популяризацию математики. Написал несколько книг о том, как решают задачи и как надо учить решать задачи.)

Уважаемые студенты,

каждый месяц у вас есть возможность попасть на бесплатный вебинар по высшей математике. Темы предстоящих вебинаров выбираем все вместе в Телеграм-канале (ТК). Переходите, кликнув по иконке

Там же будут ссылки на трансляции вебинаров за 30-60 минут до начала. Так что заходите в ТК.

Обратная матрица.

Лемма: Для любой матрицы А произведение ее на единичную матрицу, соответствующего размера, равно матрице А: АЕ=ЕА=А.

Матрица В называется обратной к матрице А, если АВ=ВА=Е. Обратная матрица к матрице А обозначается А^-1.

Обратная матрица существует только для квадратной матрицы.

Теорема: Квадратная матрица А имеет обратную тогда и только тогда, когда определитель этой матрицы отличен от нуля (|A|≠0 ).

Алгоритм нахождения обратной матрицы А^-1:

(для матриц второго и третьего порядков)

Вычислить определитель данной матрицы (|A| ).
Если |A|≠0, то переходим к пункту 3.
Если |A|=0, то обратная матрица не существует.
Вычислить все алгебраические дополнения A_ij элементов матрицы. ( Как это сделать можно посмотреть здесь)
Записать А^-1 по формуле:
для матрицы второго порядка

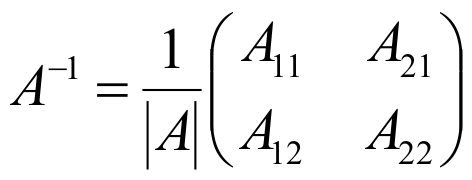
и для матрицы третьего порядка
Сделать проверку: AA^-1 =A^-1A=E.

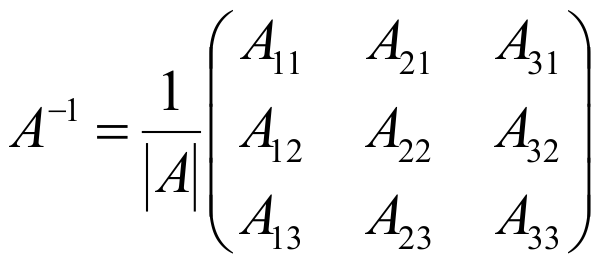
Для вычисления обратных матриц другого порядка изменится лишь формула в пункте 4.

Осталось заметить, что это не единственный способ нахождения обратной матрицы.

Найти обратную матрицу для данных матриц:

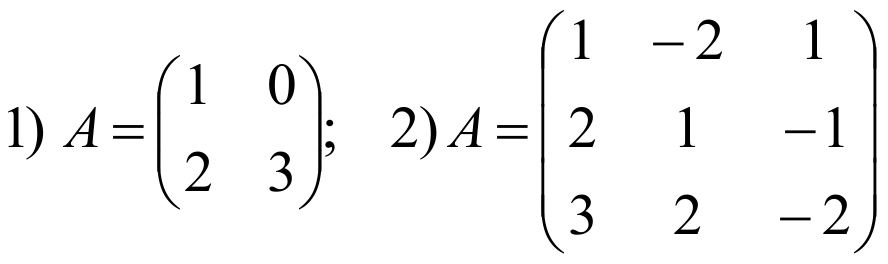
РЕШЕНИЕ:

Если Вам понравился урок и появилось желание поддержать нас, Вы можете:

отправить денежный перевод (комиссия за операцию 1%) по ссылке Ссылка на перевод.
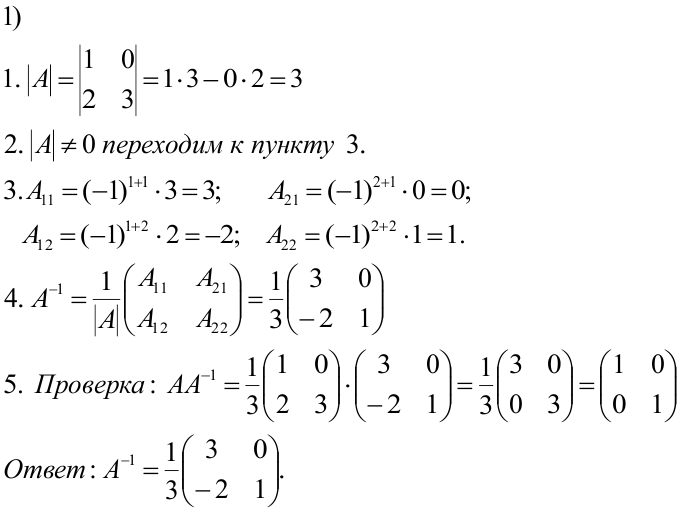
В открывшемся окне:
- поставить галочку возле «Добавить сообщение получателю»
- в появившемся поле оставить сообщение «в дар» или «подарок».
ИЛИ
оставить комментарий ниже.

Упражнения к уроку:

Найти обратную матрицу для данных матриц:

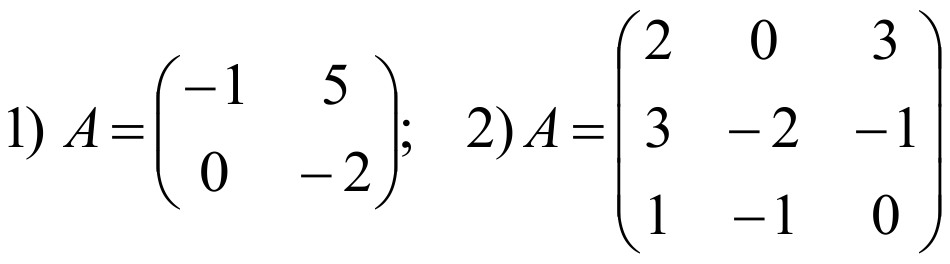
Матрицы

Показать ответ

Автор: Аникина Анна

Создан: 23.03.2014

Просмотр:44253

Комментарии к этой заметке:

Александр

22.09.2016

В задании номер 1 в упражнениях к уроку указан неправильный ответ.

Анна

11.10.2016

Спасибо, Александр! Ответы исправлены!

Добавить Ваш комментарий