Решить матричные уравнения:
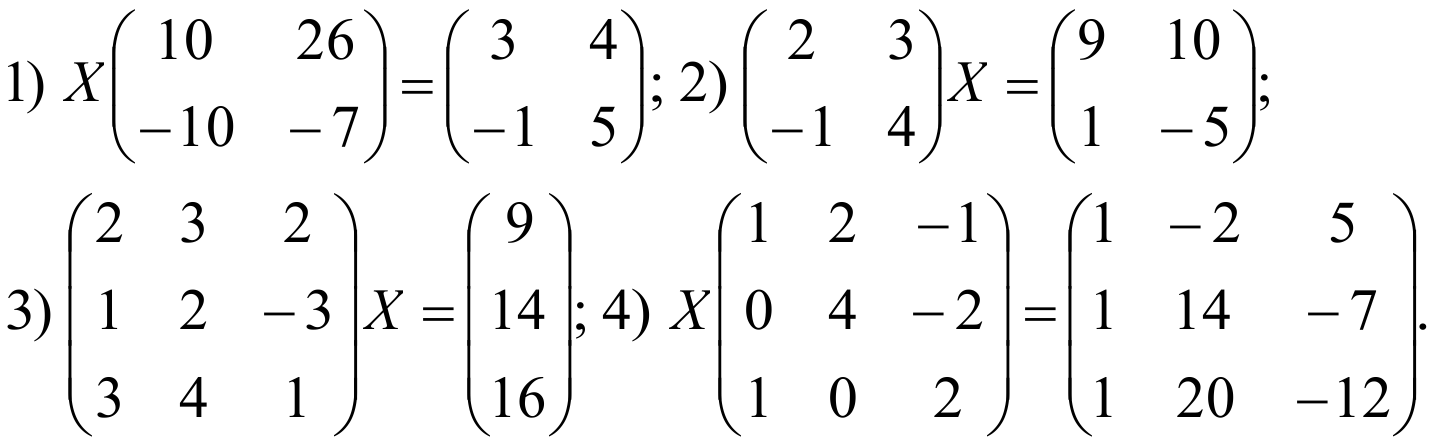

Матричные уравнения
«Если Вы хотите научиться плавать, то смело входите в воду,
а если хотите научиться решать задачи,
то решайте их.»
Д. Пойа (1887-1985 г.)
(Математик. Внёс большой вклад в популяризацию математики. Написал несколько книг о том, как решают задачи и как надо учить решать задачи.)
Там же будут ссылки на трансляции вебинаров за 30-60 минут до начала. Так что заходите в ТК.
Обратные матрицы используются при решении матричных уравнений.
Простейшими матричными уравнениями называются соотношения вида: АХ=В и ХА=В, где А,В- известные матрицы, Х – неизвестная.
Если дано уравнение вида АХ=В, то решение выглядит так Х=А-1В.
Если уравнение вида ХА=В, то Х=ВА-1.
Непосредственной подстановкой легко установить, что найденное Х является решением соответствующего уравнения.
ПРИМЕРЫ: Решить матричные уравнения.
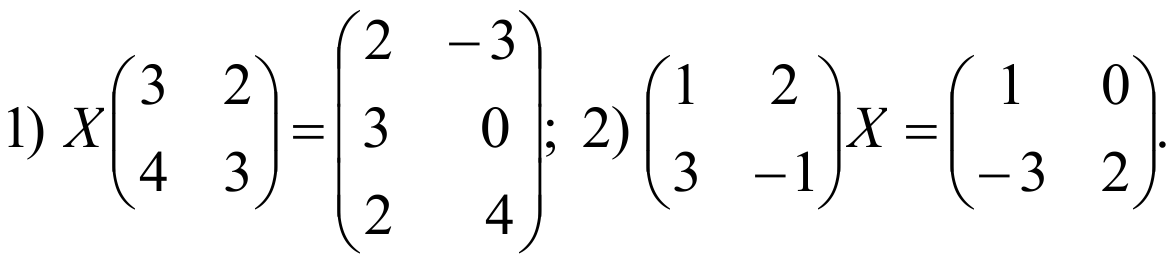
РЕШЕНИЕ:
1) Пусть
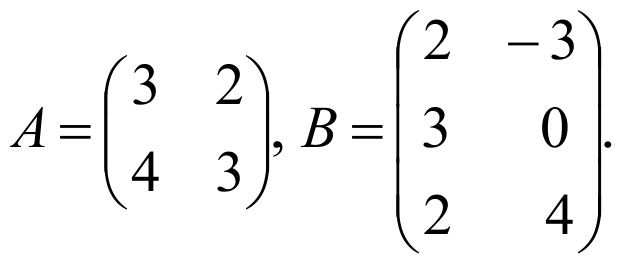
Тогда нам дано уравнение вида ХА=В, следовательно Х=ВА-1. Найдем A-1 .
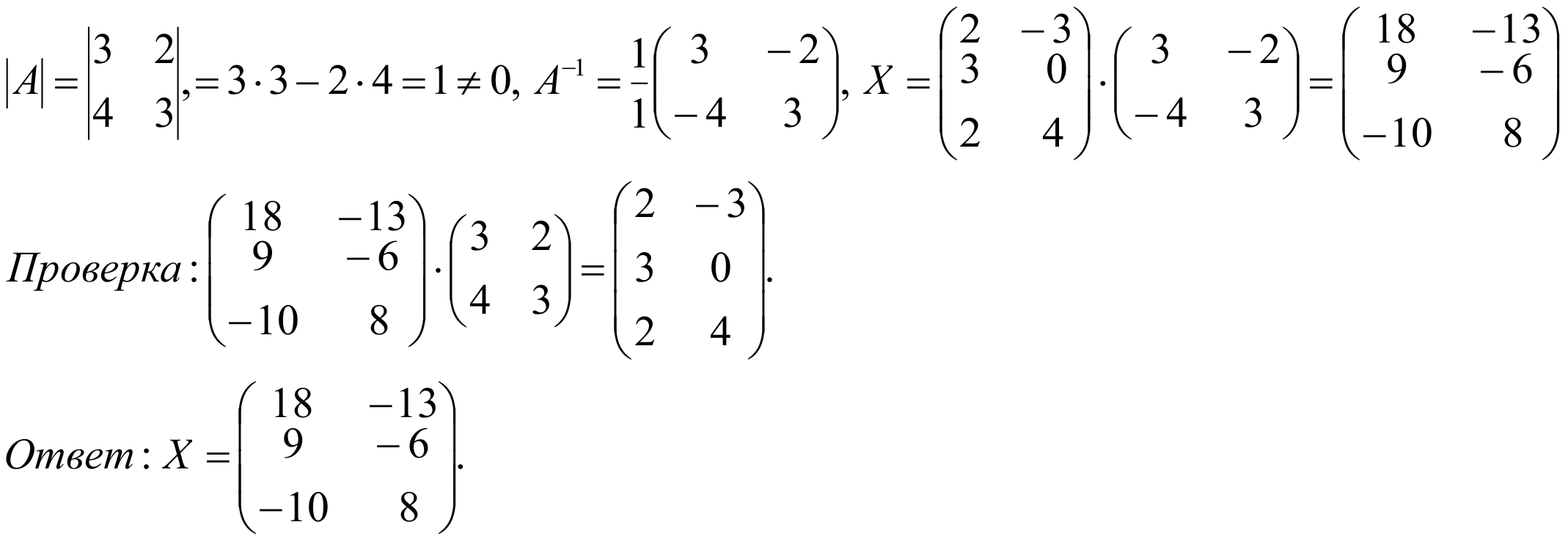
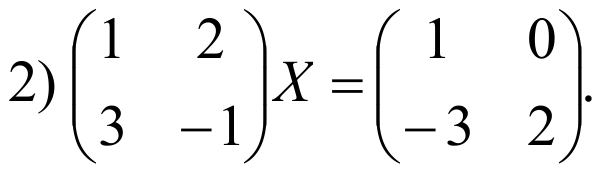
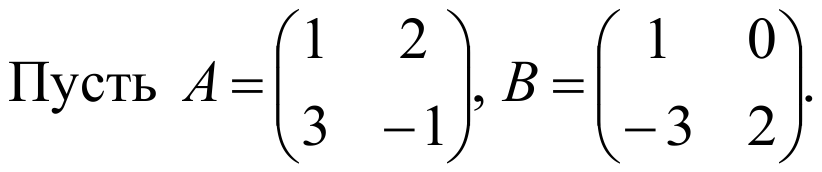
Тогда нам дано уравнение вида АX=В, следовательно Х=А-1B. Найдем A-1 .
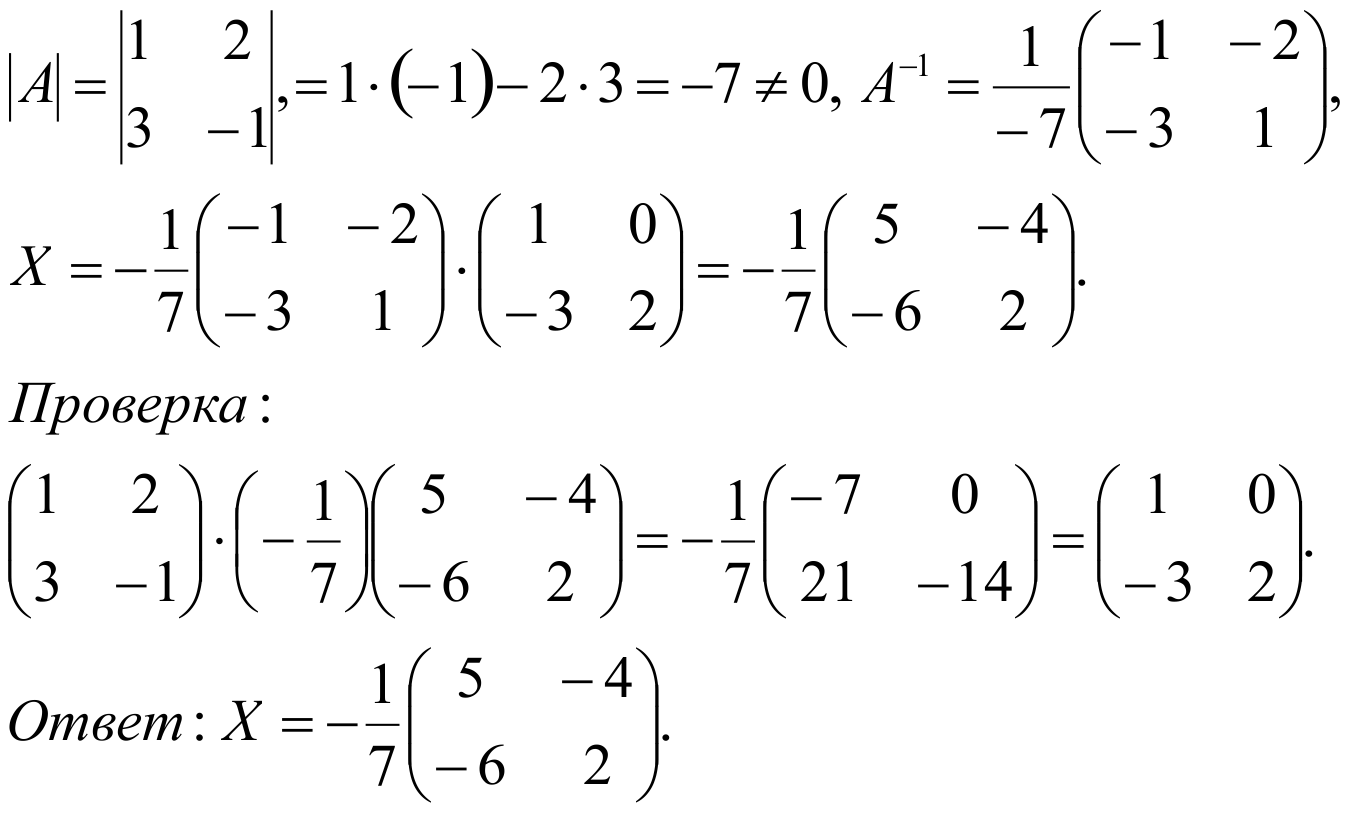
Как вычислить определитель смотреть здесь.
Как умножать матрицы можно посмотреть здесь.
Как найти обратную матрицу можно посмотреть здесь.
В открывшемся окне:
Решить матричные уравнения:
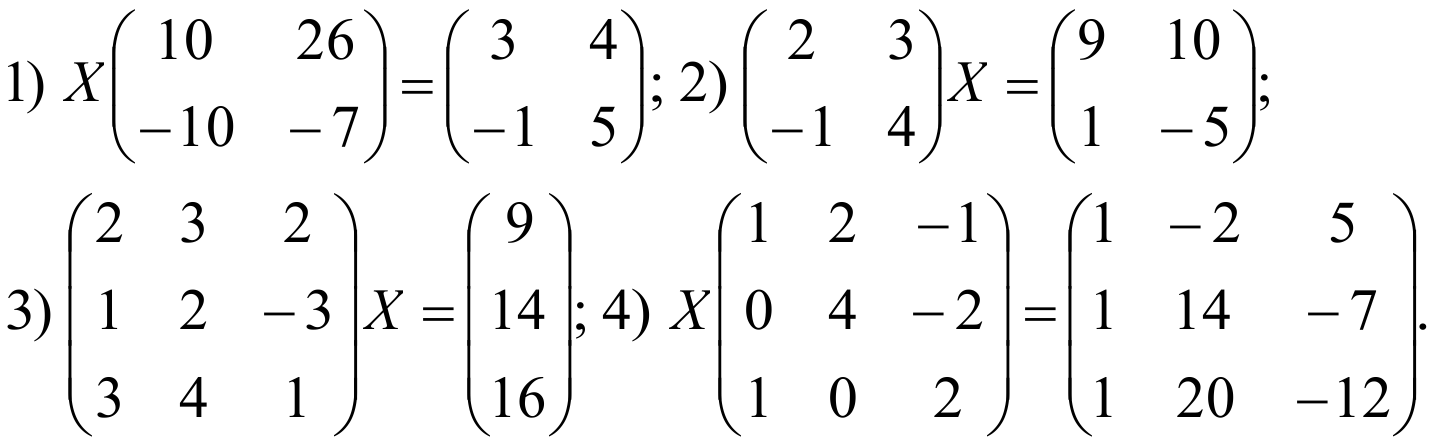
Автор: Аникина Анна
Создан: 28.03.2014
Просмотр:44272
Комментарии к этой заметке:
Как можно решить логарифм матрицы простейшем способом?
Леонид Степанович
07.03.2017
все очень хорошо. Мог бы переслать Вам ,разработанный мной калькулятор для решения матричных уравнений, но не знаю как это исполнить.Хочется узнать Ваше мнение о нем
Юля
24.03.2017
А как решить уравнение вроде ХА=В+2Х. Вот что делать с 2Х?
Анна
25.03.2017
Доброго времени суток, Юлия! Необходимо представить 2Х=Х2Е (Е-единичная матрица соответствующего размера). А далее использовать свойства действий с матрицами.
Екатерина
17.06.2017
Как решаются уравнения АХ=В, если |А|=0
Наталья
02.01.2019
А как решить уравнение ХА=В+2Х.
Добавить Ваш комментарий
Мехриниса
09.06.2015