Решите следующие системы матричным способом:
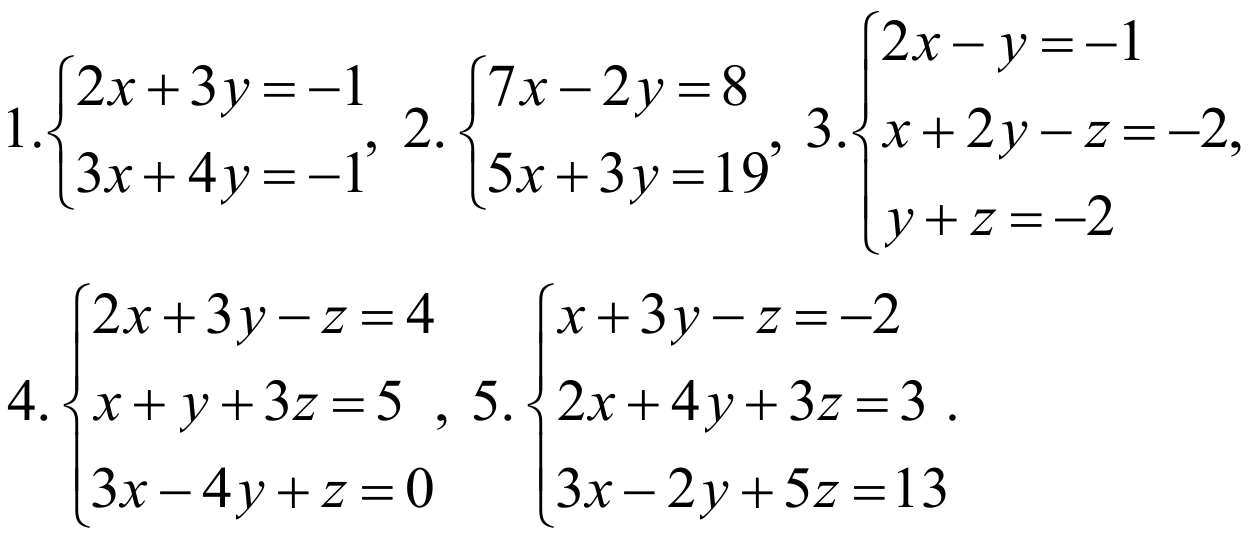
Матричный способ решения СЛУ
«Если Вы хотите научиться плавать, то смело входите в воду,
а если хотите научиться решать задачи,
то решайте их.»
Д. Пойа (1887-1985 г.)
(Математик. Внёс большой вклад в популяризацию математики. Написал несколько книг о том, как решают задачи и как надо учить решать задачи.)
Уважаемые студенты,
каждый месяц у вас есть возможность попасть на бесплатный вебинар по высшей математике. Темы предстоящих вебинаров выбираем все вместе в Телеграм-канале (ТК). Переходите, кликнув по иконке 
Там же будут ссылки на трансляции вебинаров за 30-60 минут до начала. Так что заходите в ТК.
Матричный способ решения СЛУ.
Одним из способов решения СЛУ является матричный способ. Этот способ решения СЛУ применим только при выполнении двух условий:
- Число уравнений равно числу неизвестных;
- Определитель матрицы коэффициентов при неизвестных отличен от нуля.
Теорема (матричный способ решения) Пусть дана система n линейных уравнений с n неизвестными, определитель матрицы коэффициентов А которой отличен от нуля. Тогда решение этой системы может быть получено в виде Х=А-1В, где В – матрица свободных членов, Х- матрица неизвестных.
ПРИМЕР:
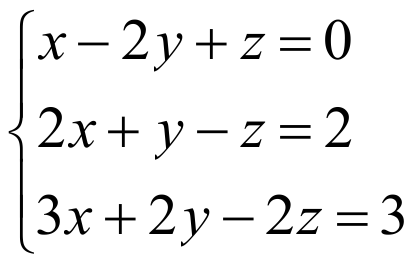
РЕШЕНИЕ:
Запишем матрицу коэффициентов А, матрицу-столбец Х (матрица-столбец неизвестных) и матрицу-столбец В (матрица-столбец свободных членов):
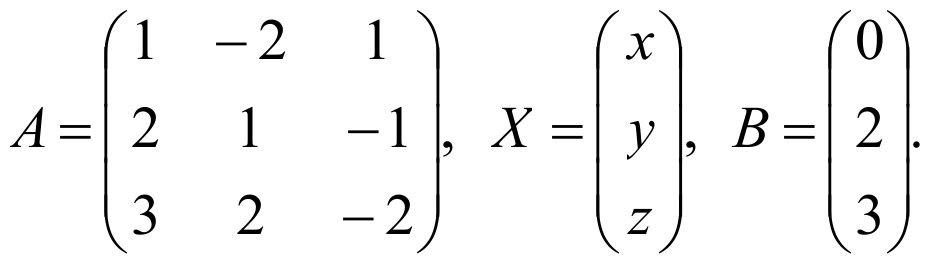
Теперь данную систему можно записать в таком виде АХ=В. Решим это матричное уравнение: Х=А-1В.
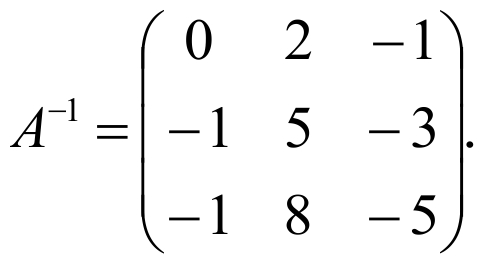
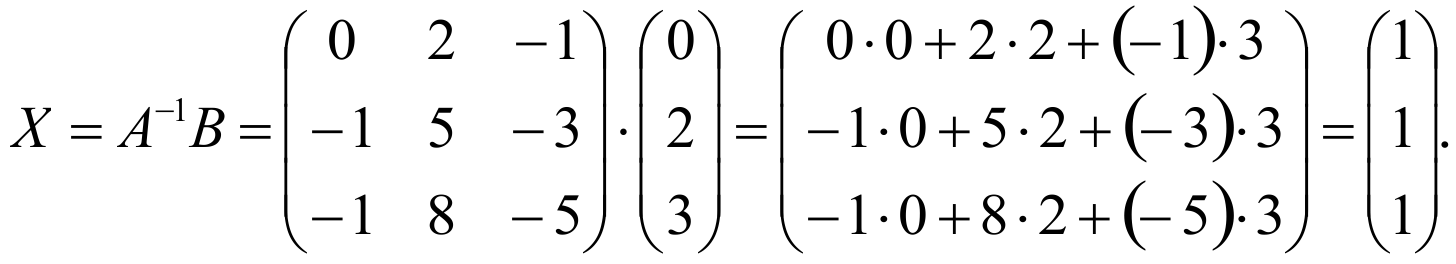
Таким образом, x=1, y=1, z=1.
ПРОВЕРКА:
Подставим в систему вместо x единицу, y единицу и z единицу.
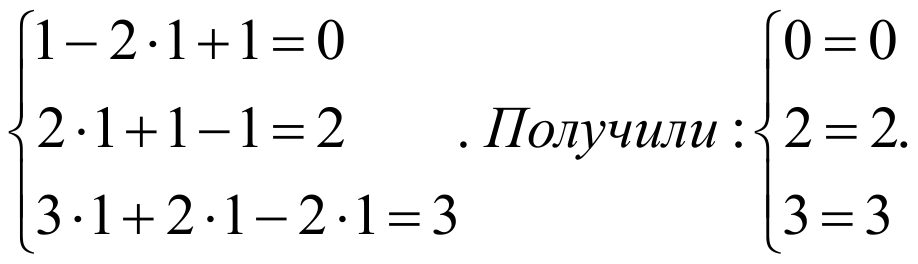
Верно. Записываем ответ.
ОТВЕТ: (1,1,1).
Если Вам понравился урок и появилось желание поддержать нас, Вы можете:
- отправить денежный перевод (комиссия за операцию 1%) по ссылке Ссылка на перевод.
В открывшемся окне:
- поставить галочку возле «Добавить сообщение получателю»
- в появившемся поле оставить сообщение «в дар» или «подарок».
ИЛИ
- оставить комментарий ниже.
Упражнения к уроку:
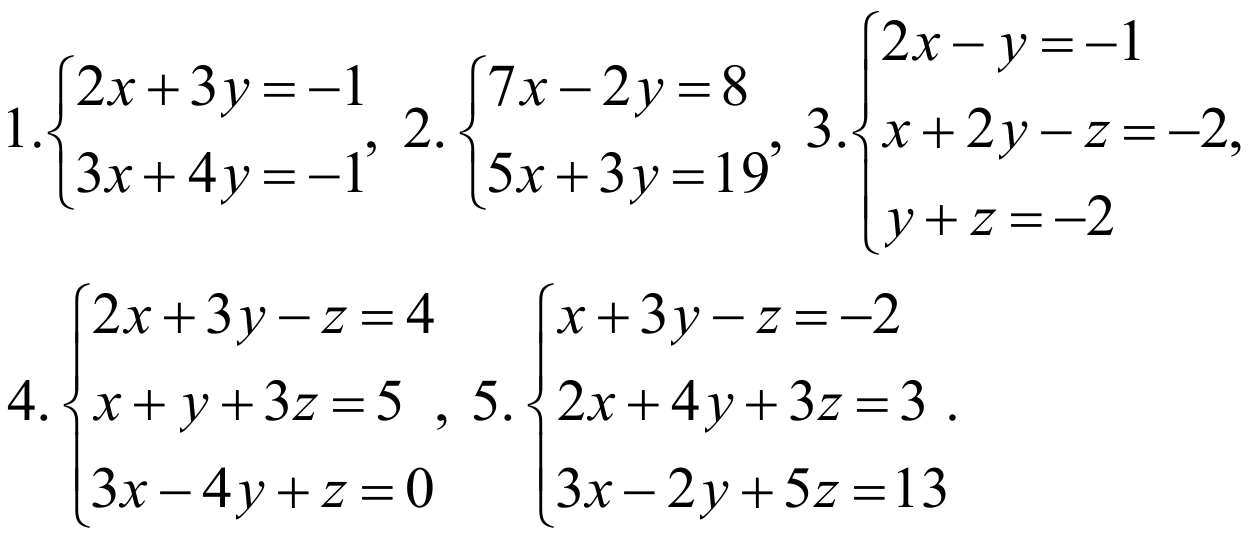
Автор: Аникина Анна
Создан: 07.04.2014
Просмотр:44212
Комментарии к этой заметке:
Добавить Ваш комментарий