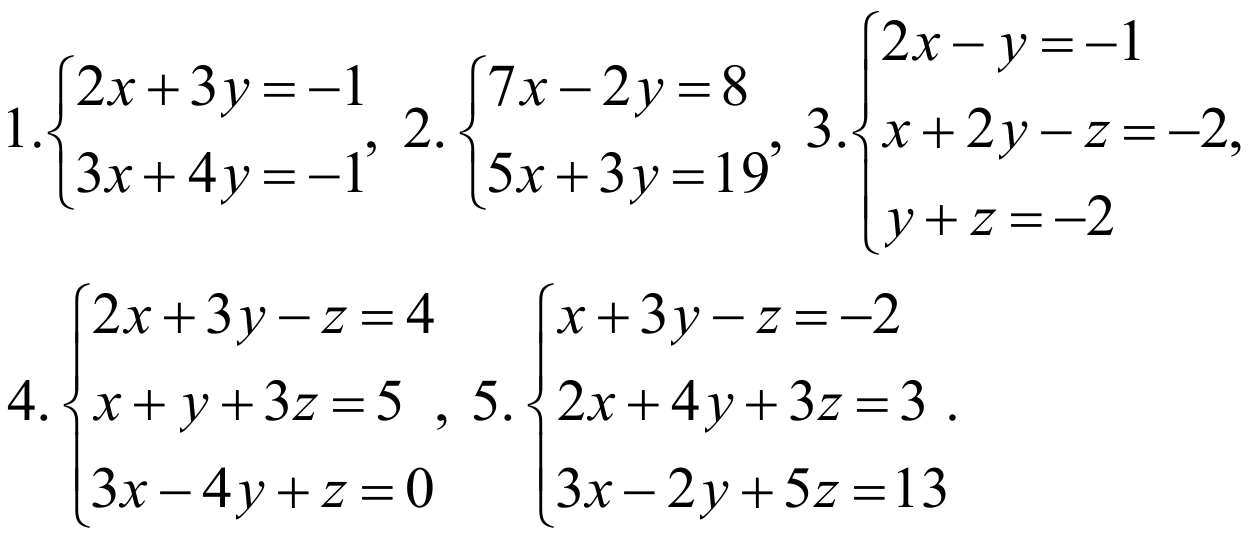
Правило Крамера

«Если Вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их.»
Д. Пойа (1887-1985 г.)

(Математик. Внёс большой вклад в популяризацию математики. Написал несколько книг о том, как решают задачи и как надо учить решать задачи.)

Уважаемые студенты,

каждый месяц у вас есть возможность попасть на бесплатный вебинар по высшей математике. Темы предстоящих вебинаров выбираем все вместе в Телеграм-канале (ТК). Переходите, кликнув по иконке

Там же будут ссылки на трансляции вебинаров за 30-60 минут до начала. Так что заходите в ТК.

Правило Крамера.

Еще один способ решения СЛУ - это правило Крамера.

Его (так же, как матричный способ решения СЛУ) применяют если:

Число уравнений равно числу неизвестных и
Определитель матрицы коэффициентов при неизвестных отличен от нуля

Если дана система двух линейных уравнений с двумя неизвестными:

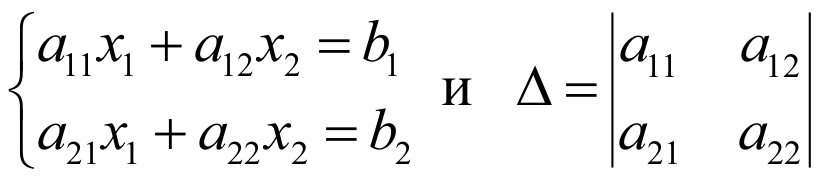
Система линейных уравнений

определитель матрицы коэффициентов,

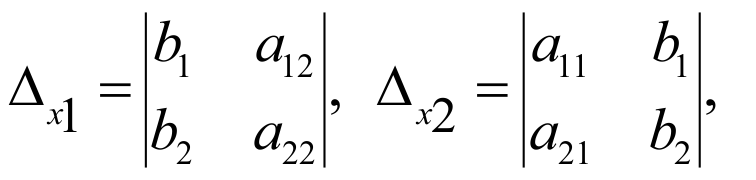
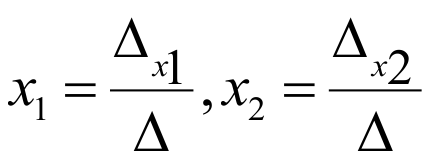
дельта х1 и х2

(получаются из определителя Δ заменой соответствующего столбца столбцом свободных членов), то если Δ ≠0, решение СЛУ может быть получено в виде:

дельта х1 и х2

Для системы трех линейных уравнений с тремя неизвестными

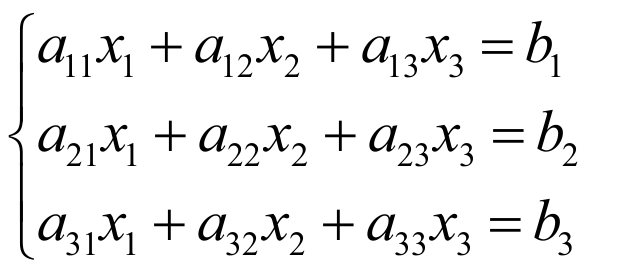
дельта х1 и х2

формулы выглядят так:

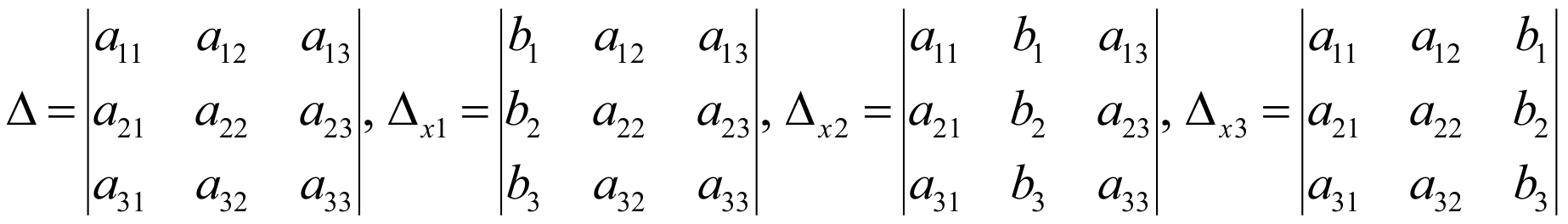Δ_x1 получается из определителя Δ заменой первого столбца столбцом свободных членов; Δ_x2 получается из определителя Δ заменой второго столбца столбцом свободных членов; Δ_x3 получается из определителя Δ заменой третьего столбца столбцом свободных членов;

ПРИМЕРЫ:

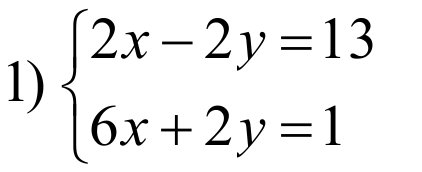
пример

РЕШЕНИЕ:

Вычислим определитель матрицы коэффициентов при неизвестных Δ

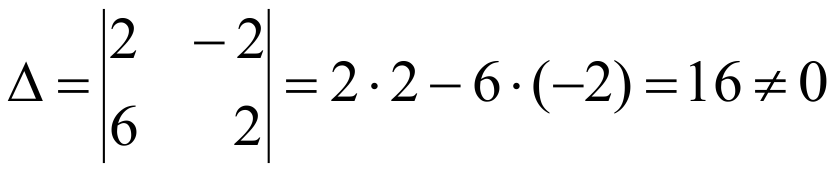определитель дельта и Δ_x, Δ_y

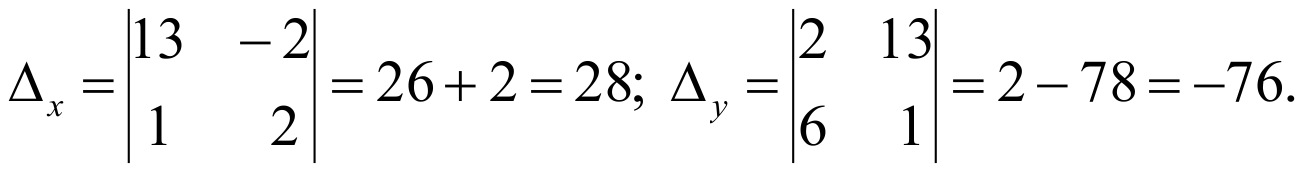
определителb дельта x, y

Δ_x получается из определителя Δ заменой первого столбца столбцом свободных членов; Δ_у получается из определителя Δ заменой второго столбца столбцом свободных членов.

x, y

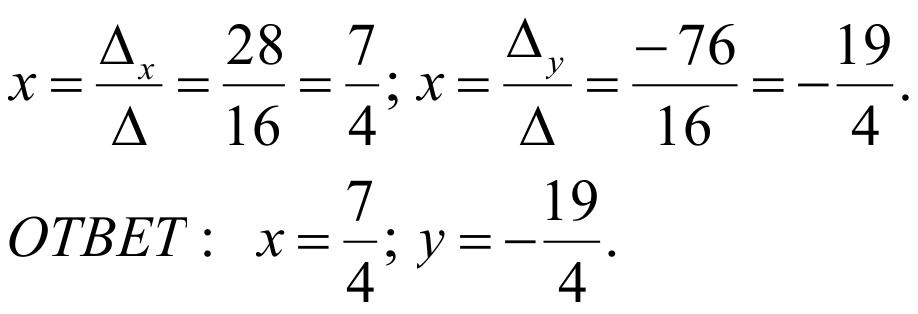
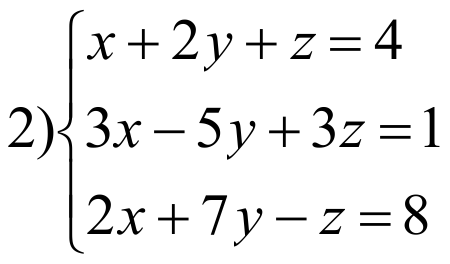
пример

РЕШЕНИЕ:

Вычислим определитель матрицы коэффициентов при неизвестных Δ,

Δ_x (получается из Δ заменой первого столбца столбцом свободных членов),

Δ_у (получается из Δ заменой второго столбца столбцом свободных членов) и

Δ_z (получается из определителя Δ заменой третьего столбца столбцом свободных членов).

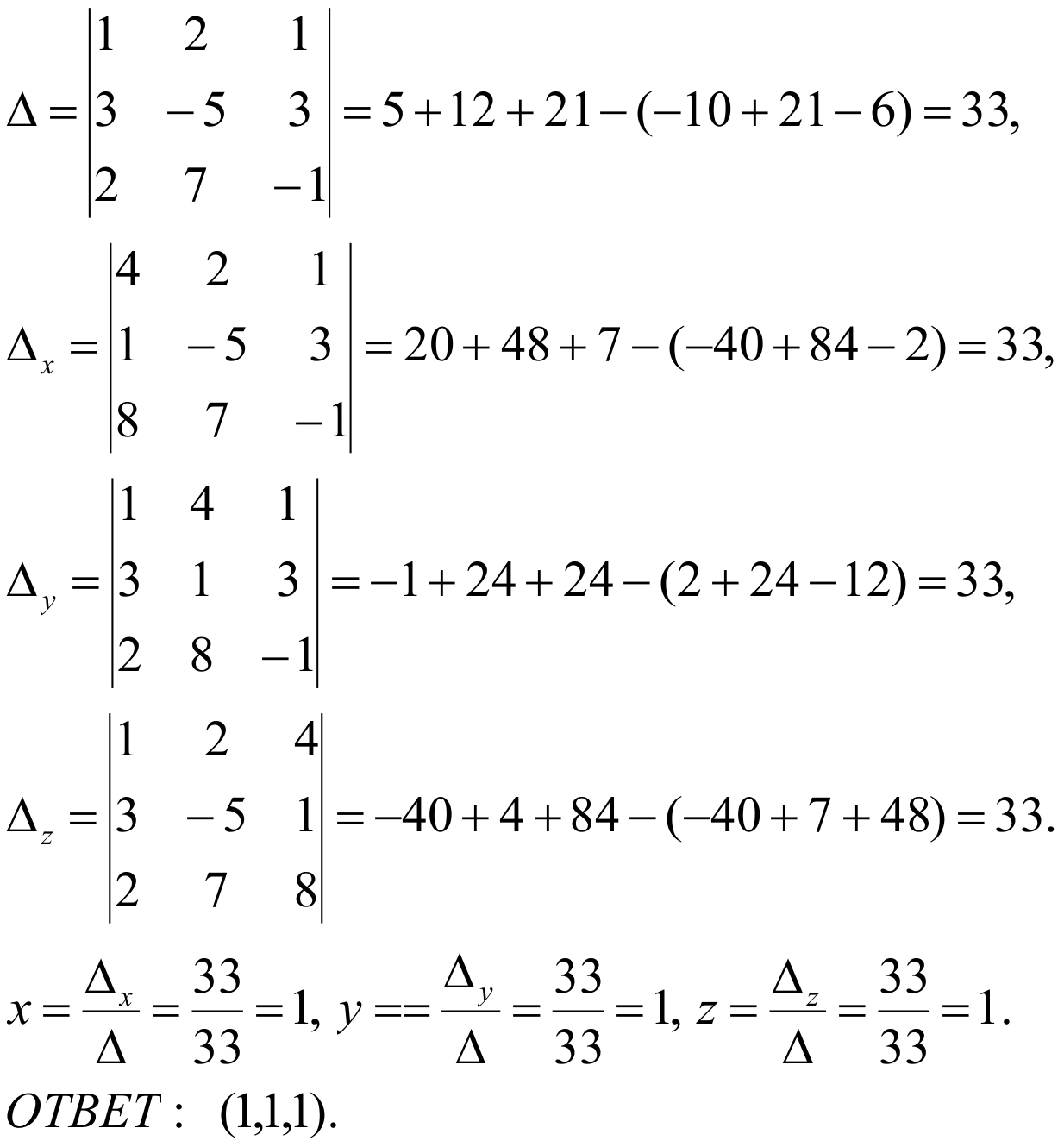
пример

При решении СЛУ для самопроверки нужно в данную систему вместо x,y,z подставить найденные значения. Если получатся все верные равенства, то СЛУ решена верно.

Если Вам понравился урок и появилось желание поддержать нас, Вы можете:

отправить денежный перевод (комиссия за операцию 1%) по ссылке Ссылка на перевод.
В открывшемся окне:
- поставить галочку возле «Добавить сообщение получателю»
- в появившемся поле оставить сообщение «в дар» или «подарок».
ИЛИ
оставить комментарий ниже.

Упражнения к уроку:

Решите следующие системы по правилу Крамера:

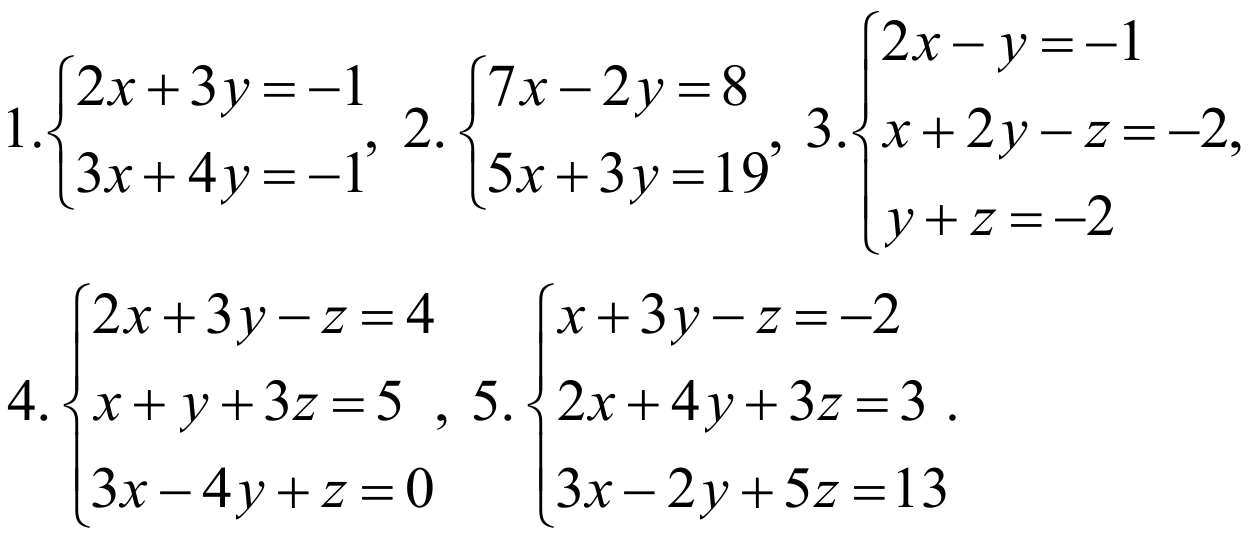
Матричные уравнения

Показать ответ

Автор: Аникина Анна

Создан: 28.04.2014

Просмотр:62140

Комментарии к этой заметке:

Наталья

23.10.2021

Здравствуйтею Хотел спросить, разбираетесь ли Вы в блок-схемах? Для лабораторной работы надо. Что-то подобное нашел, однако не уверен то ли это. <a href="https://www.mathros.net.ua/rozvjazok-systemy-linijnyh-algebraichnyh-rivnjan-metodom-kramera.html">Метод Крамера блок-схема</a> Программист из меня не очень.

Анна

24.10.2021

Здравствуйте! С методом Камера в блок-схемах не работала. В данном контексте -это метод решения системы n линейных уравнений с n неизвестными.

Наталья

25.10.2021

Спасибо за ответ. Разобралась сама. Блок-схема реализует метод Крамера для системы 3-х уравнений с 3-я неизвестными.

Добавить Ваш комментарий