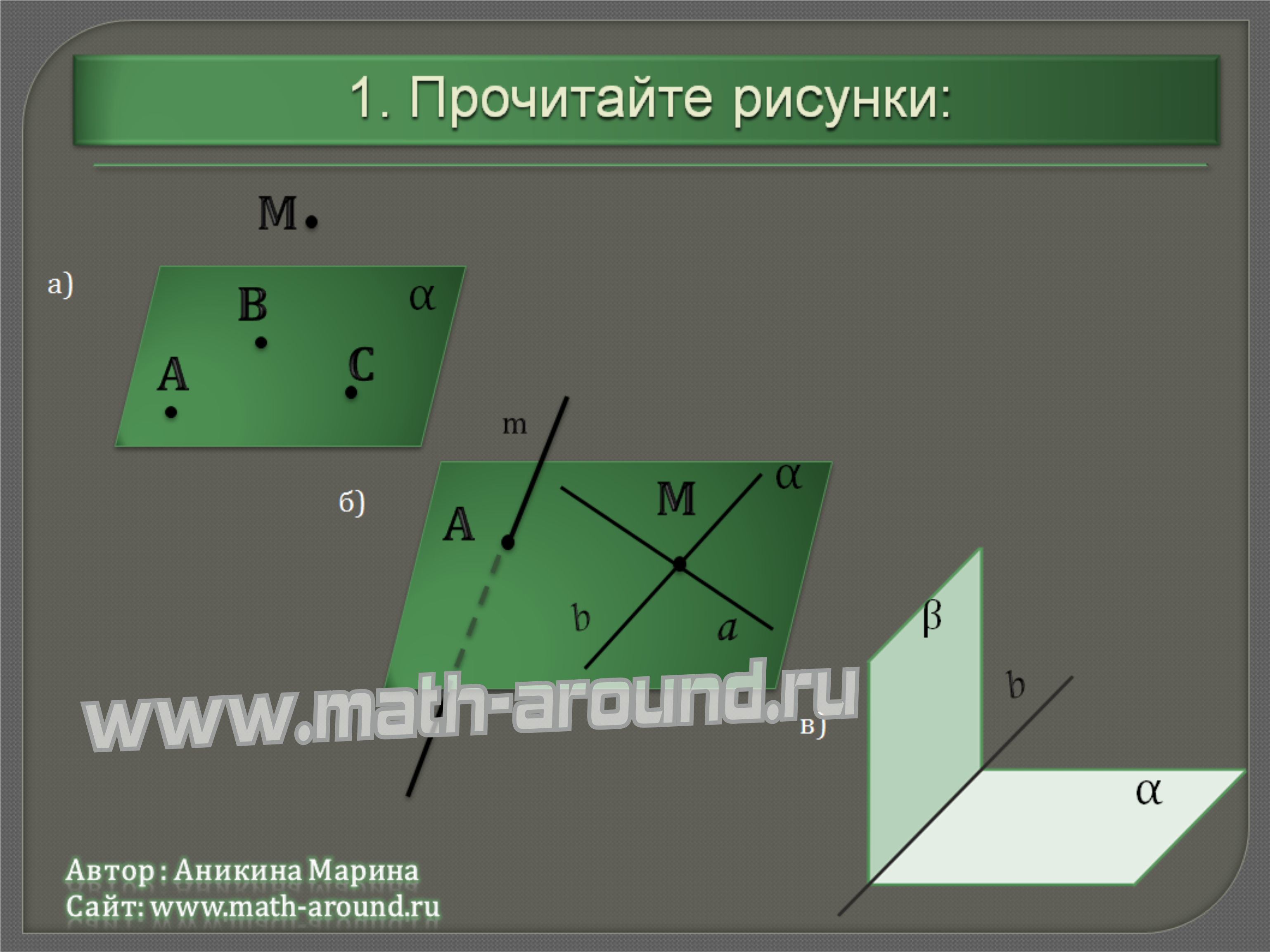
Задачи на применение аксиом стереометрии и следствий из них.

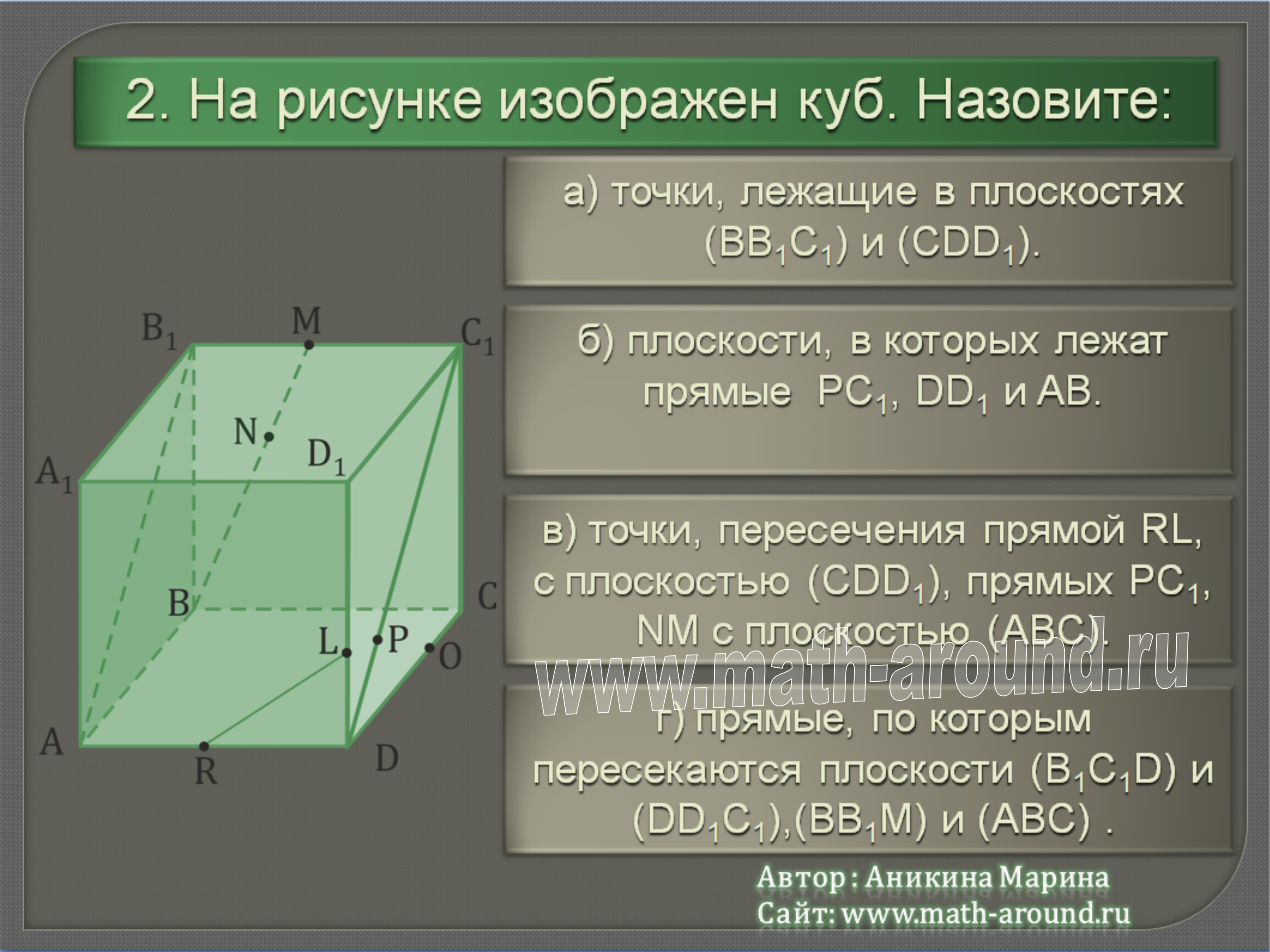
-
Найти наибольшее число плоскостей, которые можно провести через несколько точек в пространстве:
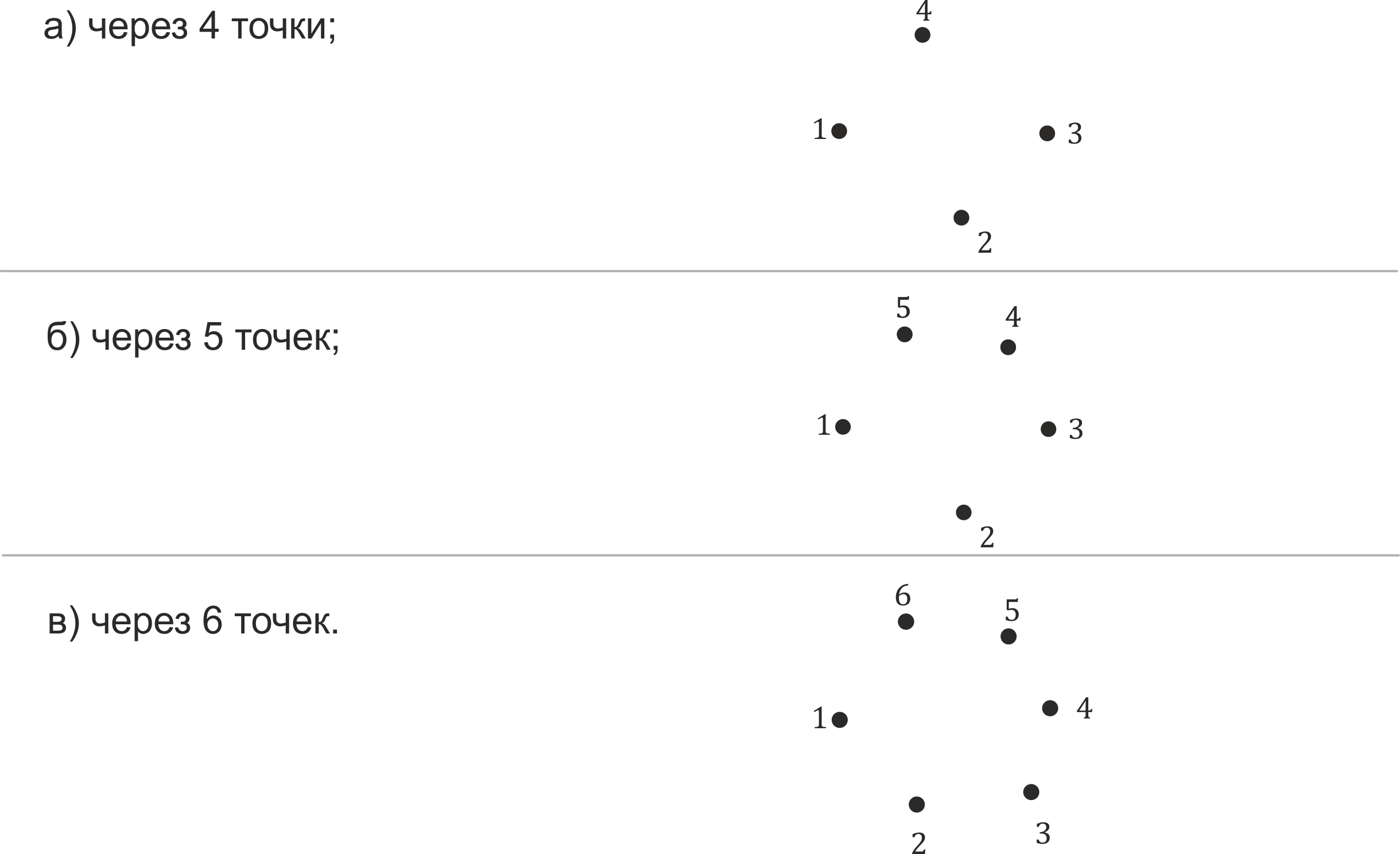
- Доказать, что все прямые, пересекающие прямую а и проходящие через точку В, не лежащую на прямой а, лежат в одной плоскости.
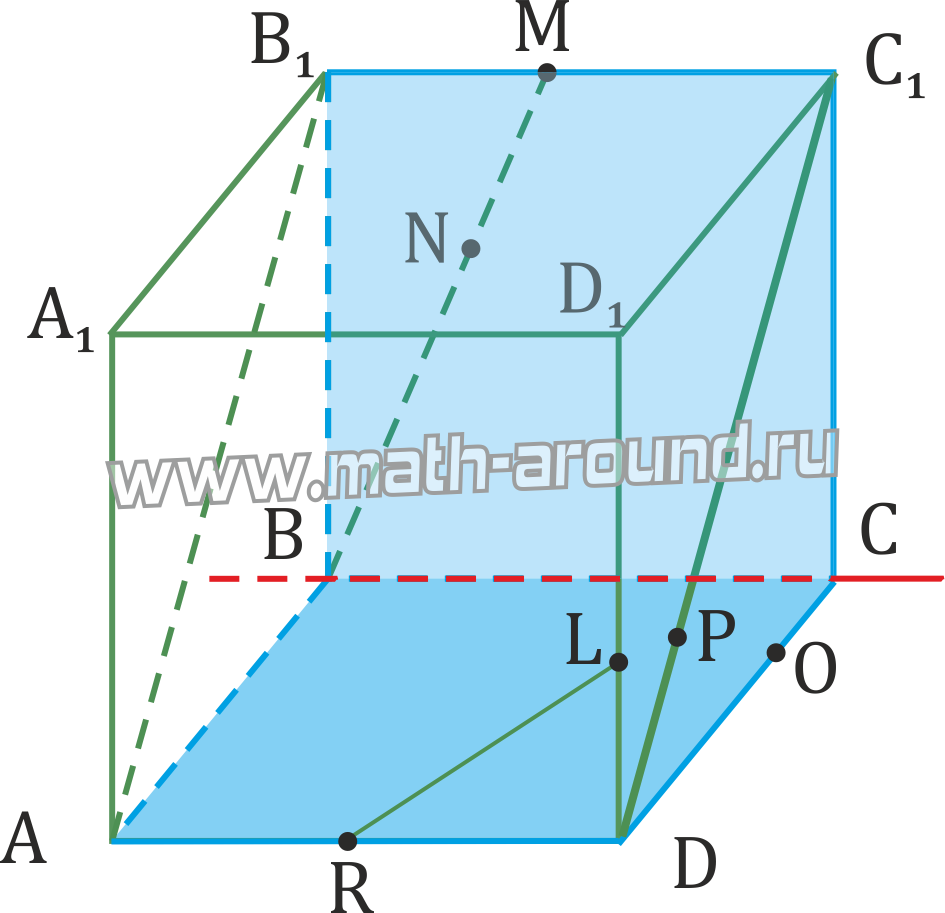
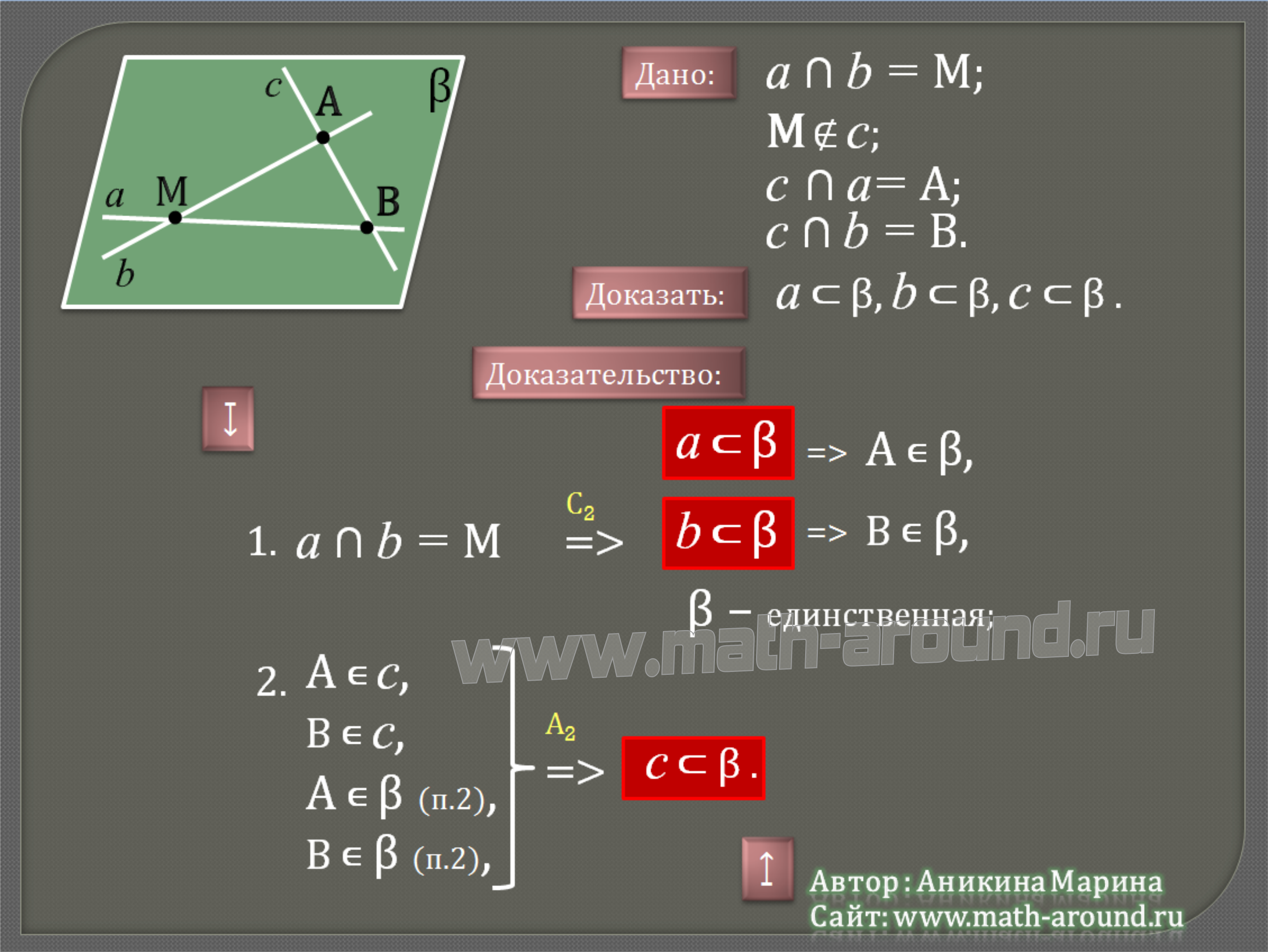
- Прямые a и b пересекаются в точке M. Прямая с, не проходящая через точку M, пересекает a и b. Доказать, что прямые a , b и c лежат в одной плоскости
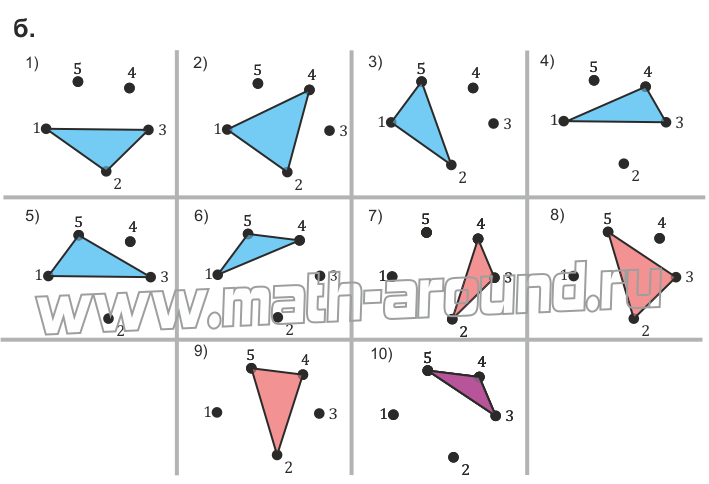
- Указать все случаи такого расположения четырех точек в пространстве, чтобы через них можно было провести плоскость и притом единственную .
- Плоскость задана тремя точками A, B и C, не лежащими на одной прямой. Необходимо построить в данной плоскости какую-нибудь прямую, не проходящую через данные точки.
- Плоскость задана прямой a и точкой M, не лежащей на этой прямой . Необходимо построить в данной плоскости произвольную прямую, отличную от прямой a и не проходящую через точку M.
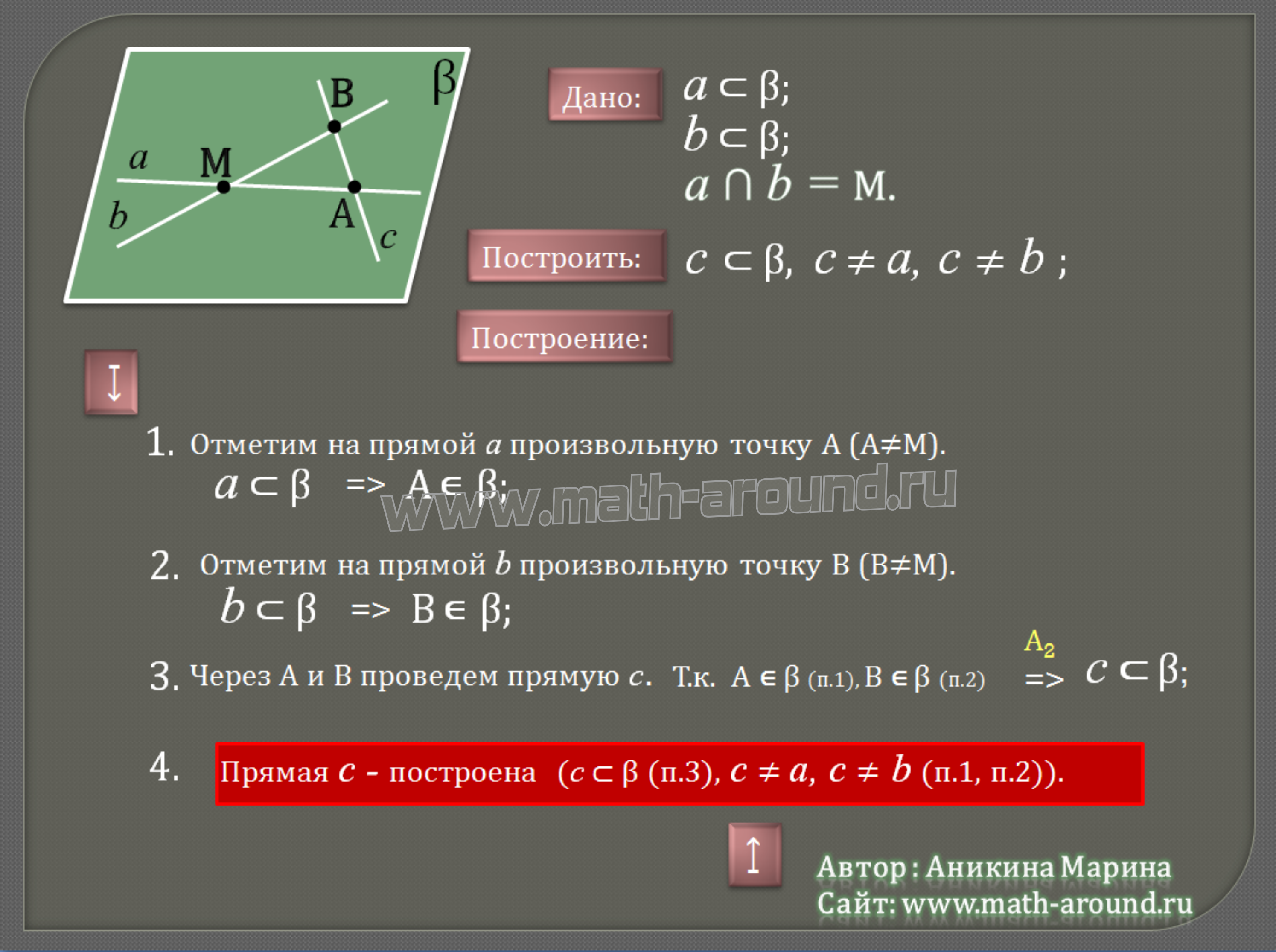
- Плоскость задана двумя пересекающимися прямыми a и b. Необходимо построить в данной плоскости произвольную прямую, отличную от данных прямых.
Если Вам понравилась информация и появилось желание поддержать нас, Вы можете:
- отправить денежный перевод с карты на карту мгновенно и без комиссий по ссылке . Ссылка на перевод . В поле «Добавьте комментарий» необходимо указать «в дар» или «подарок».
- оставить комментарий ниже.
Автор: Аникина Марина
Создан: 08.11.2013
Просмотр:44272
Комментарии к этой заметке:
Спасибо.
Ася
09.10.2016
Очень помогло, спасибо
Проскурин
02.10.2017
Спасибо
Пика
16.11.2020
Спс
Добавить Ваш комментарий









Вася
28.01.2016