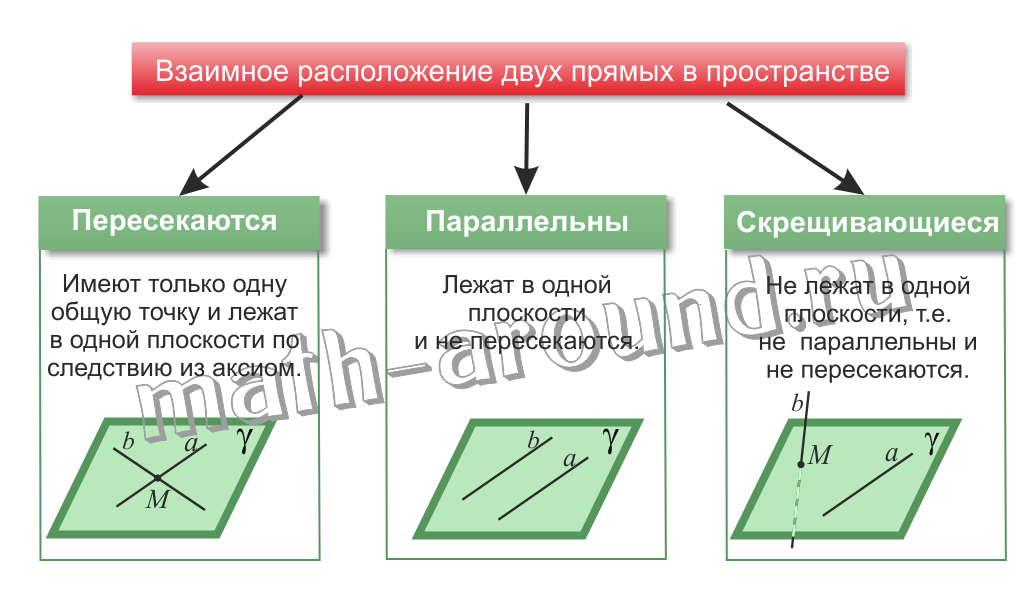
Если две прямые в пространстве параллельны или пересекаются, то они лежат в одной плоскости.
Возможен еще один случай взаимного расположения в пространстве, когда прямые не лежат в одной плоскости.

Определение. Две прямые называются скрещивающимися, если они не лежат в одной плоскости.

Представление о скрещивающихся прямых дают: 

• дороги, одна из которых проходит по эстакаде, а другая – под эстакадой;
• детская горка, где одна из скрещивающихся прямых – самая нижняя ступенька лесенки, а вторая – бортик самой горки;
• телеграфные провода и провода антенны.

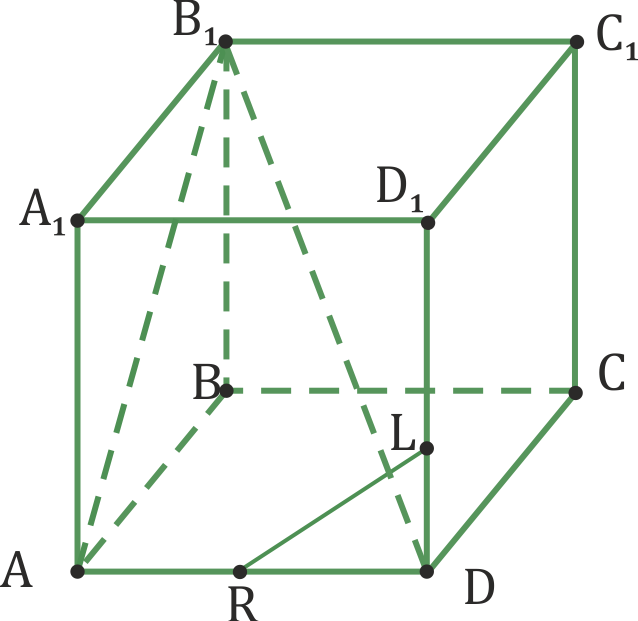
К кубе АВСDА₁В₁С₁D₁ прямые A₁D₁ и ВВ₁,  AB и B₁C₁,  В₁D и  ВC, RL и BC, AB₁ и D₁C₁  являются скрещивающимися.

Признак  скрещивающихся прямых.

Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.

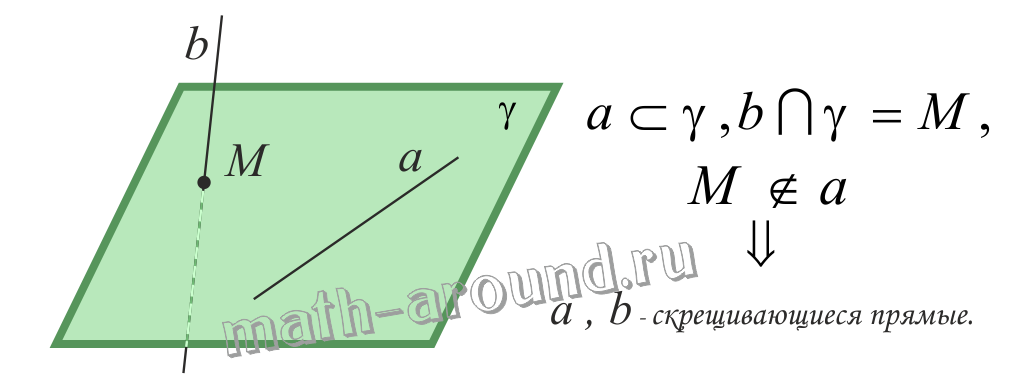
Теорема о скрещивающихся прямых.

Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.