Вводный урок в курс линейной алгебры
«Если Вы хотите научиться плавать, то смело входите в воду,
а если хотите научиться решать задачи,
то решайте их.»
Д. Пойа (1887-1985 г.)
(Математик. Внёс большой вклад в популяризацию математики. Написал несколько книг о том, как решают задачи и как надо учить решать задачи.)
Уважаемые студенты,
каждый месяц у вас есть возможность попасть на бесплатный вебинар по высшей математике. Темы предстоящих вебинаров выбираем все вместе в Телеграм-канале (ТК). Переходите, кликнув по иконкеТам же будут ссылки на трансляции вебинаров за 30-60 минут до начала. Так что заходите в ТК.
Вводный урок в курс линейной алгебры
Фокусы с матрицами
- отправить денежный перевод по кнопке
ИЛИ
- оставить комментарий ниже.
Матрица, её история.
Впервые матрица упоминалась ещё в древнем Китае, называясь тогда «магическим квадратом» (ок. 2200 лет до н.э.).
Теория определителей развивалась в конце XVII-го века. Габриэль Крамер начал разрабатывать свою теорию в XVIII-ом столетии и опубликовал правило Крамера в 1751 году. Примерно в этом же промежутке времени появился метод Гаусса. Теория матриц начала своё существование в середине XIX века в работах У. Гамильтона и А. Кэли. Фундаментальные результаты в теории матриц принадлежат Вейерштрассу, Жордану, Фробениусу. Термин «матрица» ввел Дж. Сильвестр в 1850 г.
К середине XIX в. матрицы стали самостоятельными объектами математических исследований. К этому времени были сформулированы правила сложения и умножения матриц. Основную роль в их разработке сыграли работы Гамильтона, Кэли и Сильвестра. Современное обозначение матрицы предложил Кэли в 1841 году. Исследования Вейерштрасса и Фробениуса далеко продвинули теорию матриц, обогатив ее новым содержанием.
Сейчас матрицы широко применяются в математике для компактной записи систем линейных алгебраических или дифференциальных уравнений. В этом случае, количество строк матрицы соответствует числу уравнений, а количество столбцов — количеству неизвестных. В результате решение систем линейных уравнений сводится к операциям над матрицами.
Всю таблицу умножения можно представить в компактной матричной форме, как результат произведения матриц
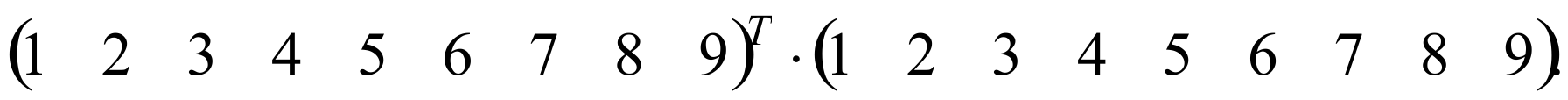
Автор: Аникина Анна
Создан: 12.10.2013
Просмотр:62077
Комментарии к этой заметке:
Добавить Ваш комментарий
