1. Параллельные прямые в пространстве.

Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Обозначение параллельных прямых a и b: a || b.

Теорема о параллельных прямых.

Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.

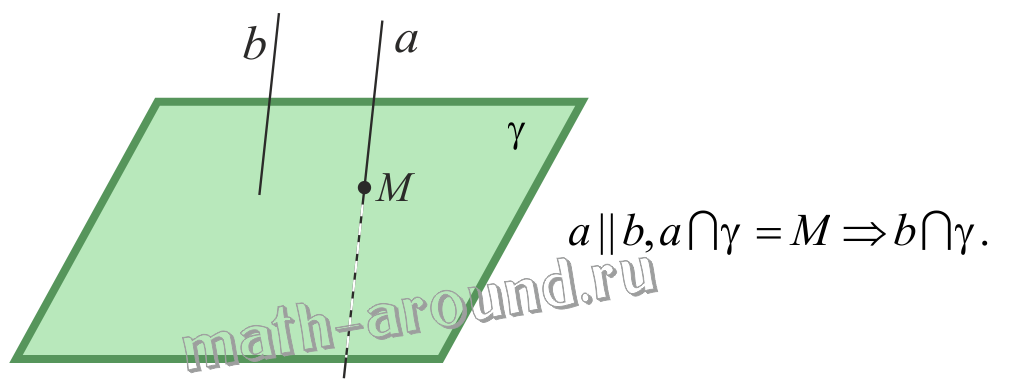
Лемма о пересечении плоскости параллельными прямыми.

Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

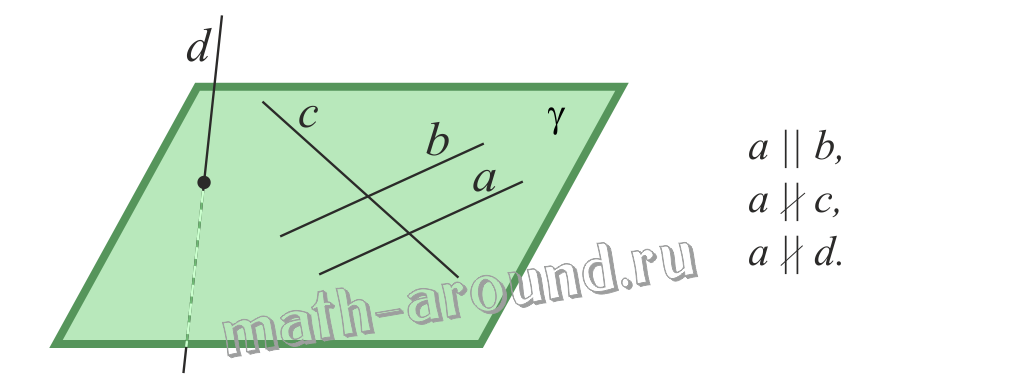
Теорема о параллельности трех прямых.

Если две прямые параллельны третьей прямой, то они параллельны.

2. Параллельность прямой и плоскости.

Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек.

Обозначение параллельности прямой a и плоскости β: a || β.

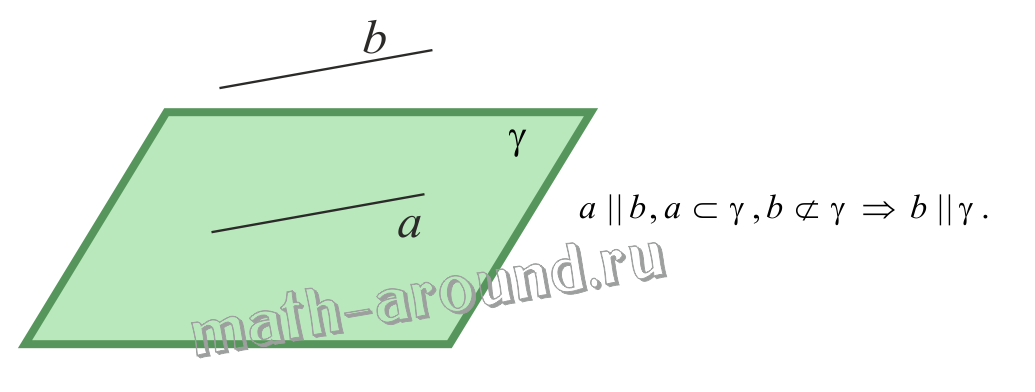
Признак параллельности прямой и плоскости.

Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.

Два утверждения, которые часто используются при решении задач.

1. Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.

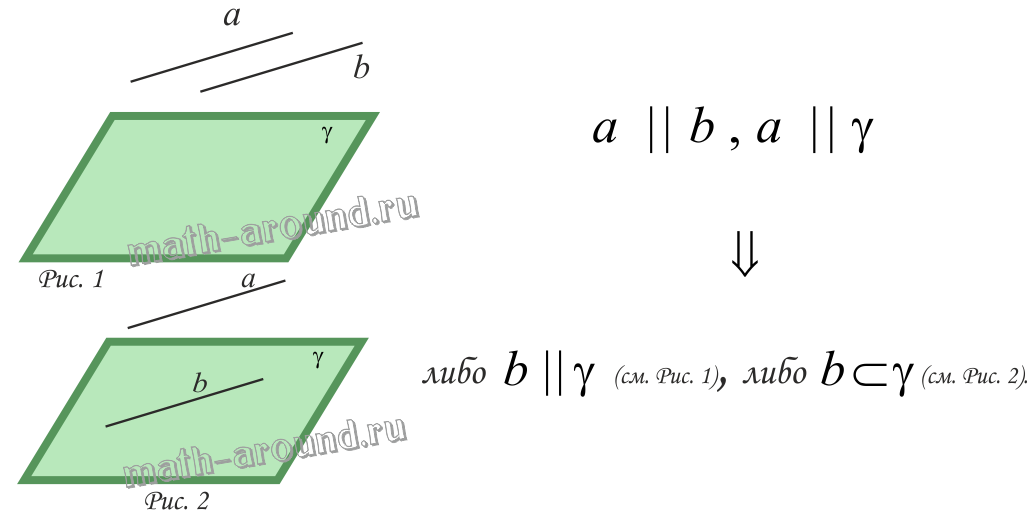
2. Если одна из двух параллельных прямых параллельна данной плоскости, то и другая прямая либо также параллельна плоскости, либо лежит в этой плоскости.

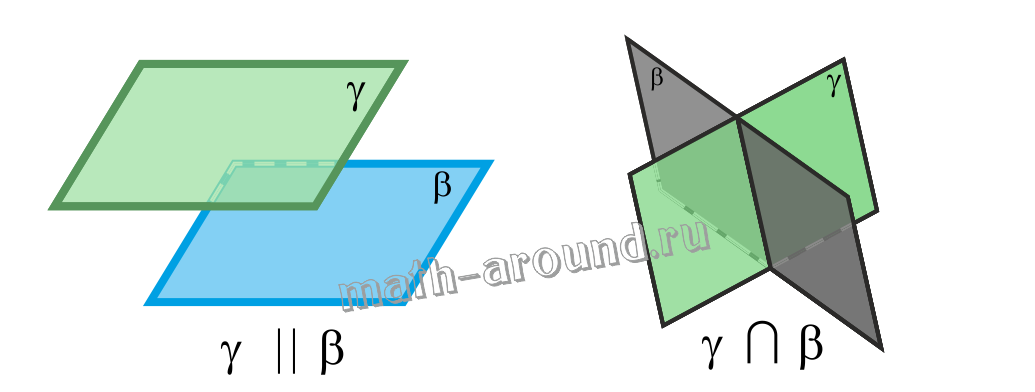
3. Параллельность плоскостей.

Определение. Две плоскости называются параллельными, если они не пересекаются.

Обозначение параллельных плоскостей γ и β: γ||β.

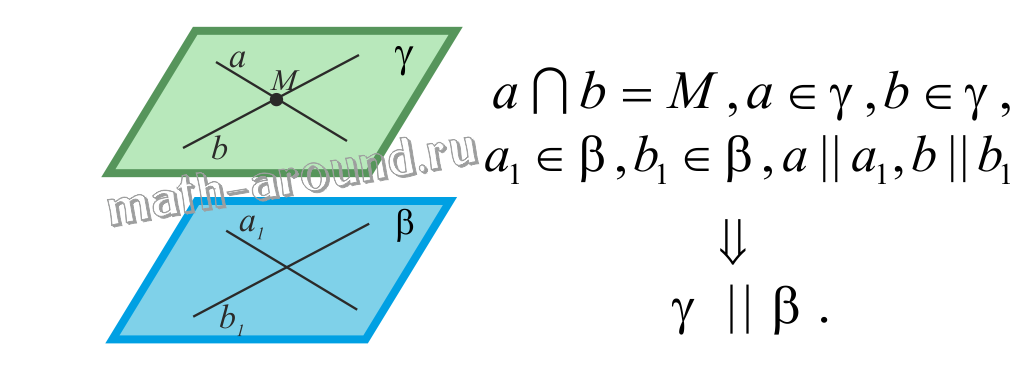
Признак параллельности двух плоскостей.

Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.

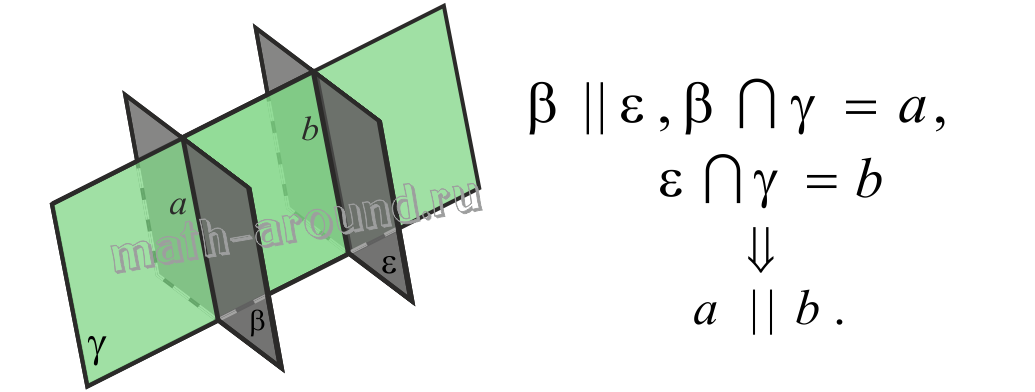
Свойства параллельных плоскостей:

1. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.

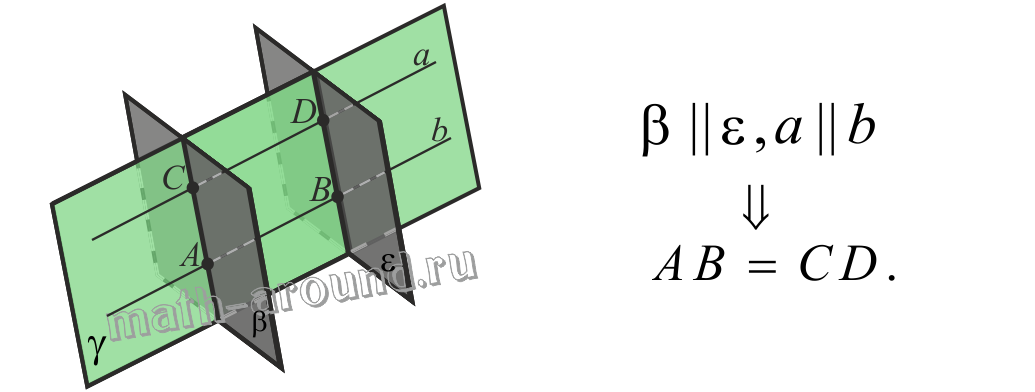
2. Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.