Определение. Призма - это многогранник, все вершины которого расположены в двух параллельных плоскостях, причем в этих же двух плоскостях лежат две грани призмы, представляющие собой равные многоугольники с соответственно параллельными сторонами, а все ребра, не лежащие в этих плоскостях, параллельны.

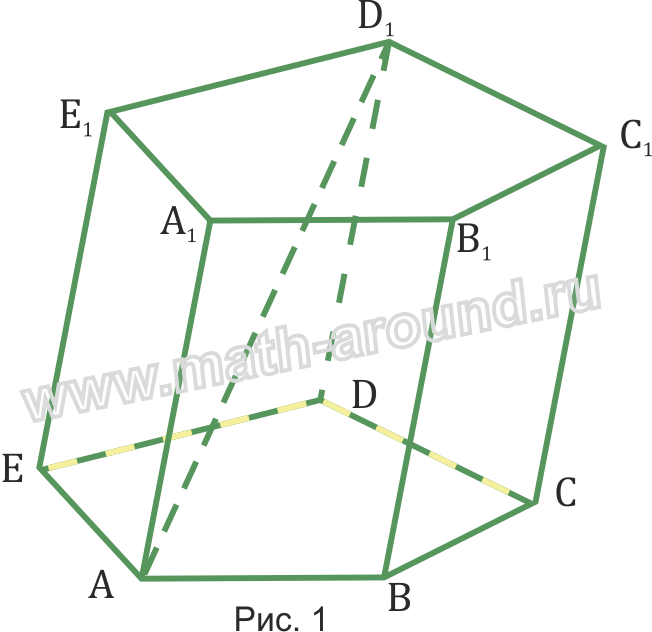Две равные грани называются основаниями призмы (ABCDE, A₁ B₁C₁D₁E₁).

Все боковые грани образуют боковую поверхность призмы.

Все боковые грани призмы являются параллелограммами.  

Ребра, не лежащие в основаниях, называются боковыми ребрами призмы(AA₁, BB₁, CC₁, DD₁, EE₁).

Диагональю призмы называется отрезок, концами которого служат две вершины призмы, не лежащие на одной ее грани (АD₁).

Длина отрезка, соединяющего основания призмы и перпендикулярного одновременно обоим основаниям,называется высотой призмы.

Обозначение: ABCDE A₁ B₁C₁D₁E₁. (Сначала в порядке обхода указывают вершины одного основания, а затем в том же порядке - вершины другого; концы каждого бокового ребра обозначают одинаковыми буквами, только вершины, лежащие в одном основании, обозначаются буквами без индекса, а в другом - с индексом)

Название призмы связывают с числом углов в фигуре, лежащей в ее основании, например, на рисунке 1 в основании лежит пятиугольник, поэтому призму называют пятиугольной призмой. Но т.к. у такой призмы 7 граней, то она семигранник (2 грани - основания призмы, 5 граней - параллелограммы, - ее боковые грани)

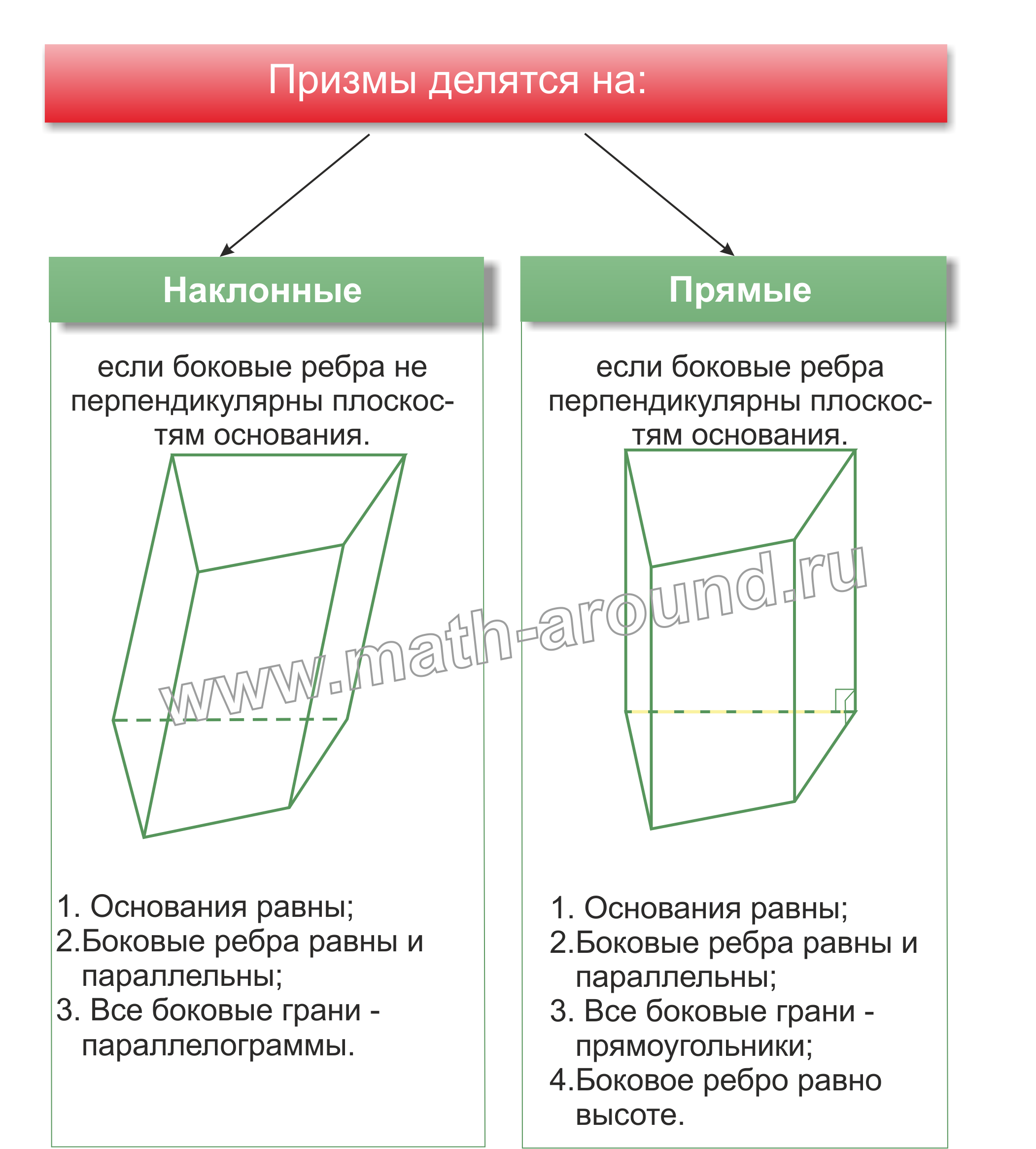
Среди прямых призм выделяется частный вид: правильные призмы.

Прямая призма называется правильной, если ее основания-правильные многоугольники.

У правильной призмы все боковые грани равные прямоугольники.

Частным случаем призмы является параллелепипед.

Параллелепипед

Параллелепипед - это четырехугольная призма, в основании которой лежит параллелограмм (наклонный параллелепипед).

Прямой параллелепипед - параллелепипед, у которого боковые ребра перпендикулярны плоскостям основания.

Прямоугольный параллелепипед - прямой параллелепипед, основанием которого является прямоугольник .

Свойства и теоремы:

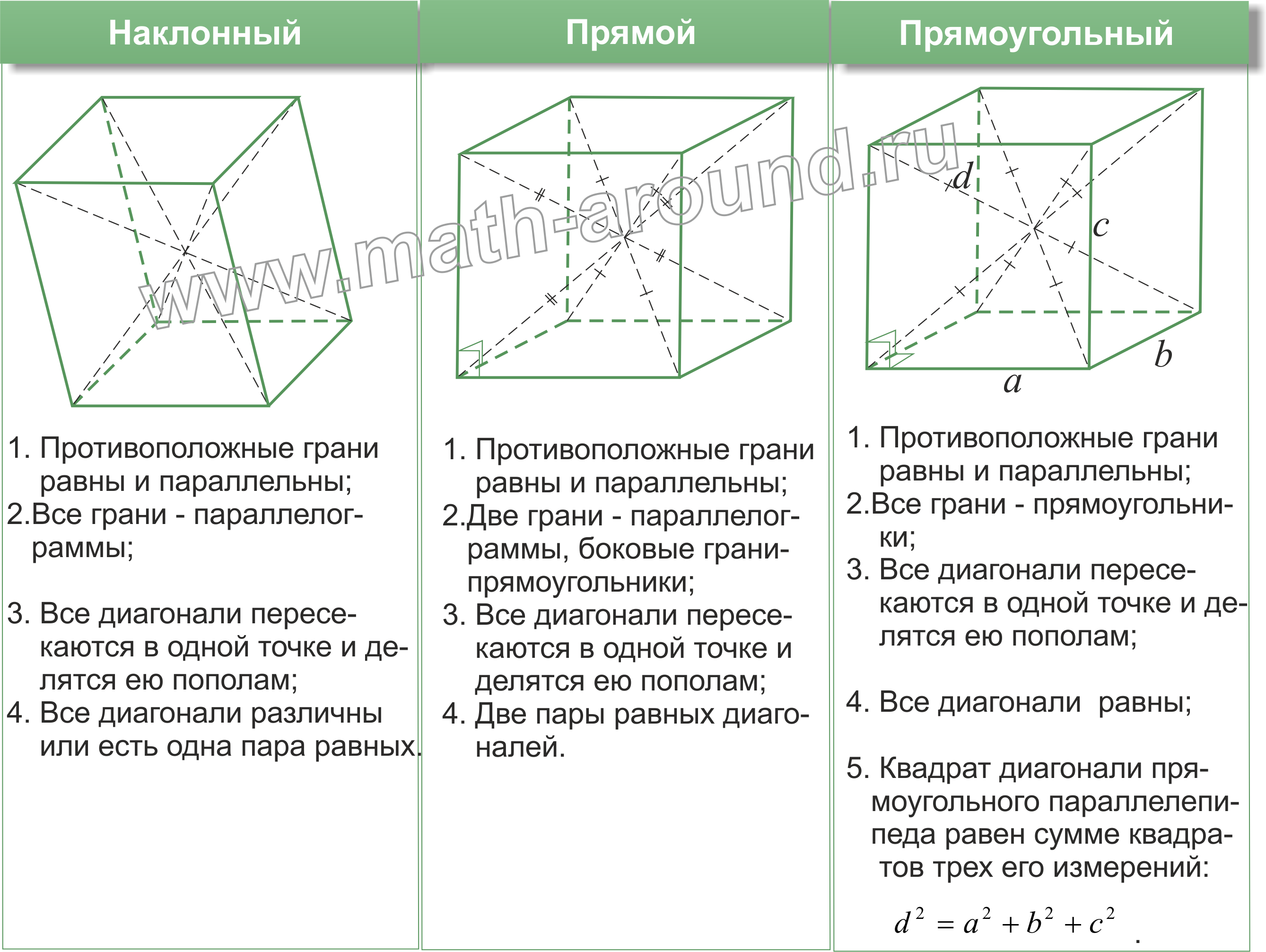
Некоторые свойства параллелепипеда аналогичны известным свойствам параллелограмма.

Прямоугольный параллелепипед, имеющий равные измерения, называются кубом.

У куба все грани равные квадраты.

Квадрат диагонали, равен сумме квадратов трех его измерений

,

где d - диагональ квадрата;
a - сторона квадрата.

Представление о призме дают: 

• различные архитектурные сооружения;
• детские игрушки;
• упаковочные коробки;
• дизайнерские предметы и т.д.