Нахождение угла между прямой и плоскостью.
Давайте повторим определение угла между прямой и плоскостью.
Определение. Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется угол между прямой и ее проекцией на плоскость.
Пусть даны плоскость γ и прямая a, которая пересекает эту плоскость и не перпендикулярна к ней.
Построим угол между прямой a и плоскостью γ:
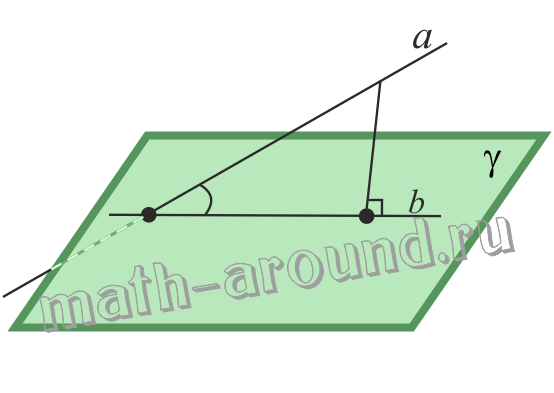
- Из любой удобной для нас точки прямой a опустим перпендикуляр к плоскости γ;
- Через точки оснований наклонной и перпендикуляра проведем прямую b . Прямая b - проекция прямой a на плоскость γ;
- Острый угол между прямыми a и b – это угол между прямой a и плоскостью γ, т.е. ∠(a;b)= ∠(a;γ) , где ∠(a;b) - угол между прямыми а и b; ∠(a;γ) - угол между прямой а и плоскостью γ.
Для решения задач с помощью метода координат нам необходимо вспомнить следующее:
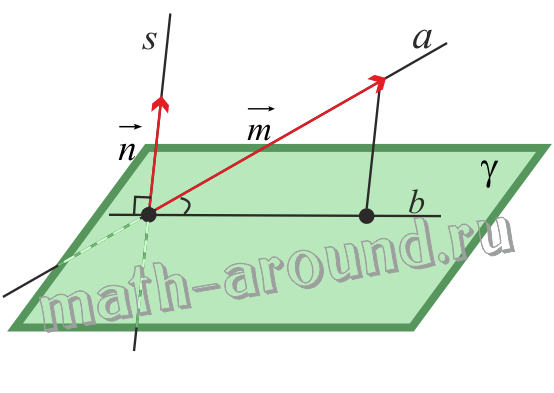
- Направляющим вектором прямой a называется ненулевой вектор
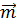 , который лежит либо на прямой a, либо на прямой , параллельной a;
, который лежит либо на прямой a, либо на прямой , параллельной a; - Вектор нормали – это ненулевой вектор
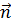 , перпендикулярный плоскости γ. Прямая s, на которой лежит вектор нормали, перпендикулярна плоскости γ;
, перпендикулярный плоскости γ. Прямая s, на которой лежит вектор нормали, перпендикулярна плоскости γ;
3. Если известны координаты направляющего вектора ![]() { a1; b1; c1} и вектора нормали
{ a1; b1; c1} и вектора нормали
![]() {a; b; c}, то угол между прямой а и плоскостью γ вычисляется по формуле, которую сейчас выведем.
{a; b; c}, то угол между прямой а и плоскостью γ вычисляется по формуле, которую сейчас выведем.
Нам известна формула нахождения угла между прямыми:
![]() ; (1)
; (1)
∠(s; a) = 90°-∠(a;b), тогда cos∠(s;a)=cos (90°-∠(a;b))=sin ∠(a;b) ; (2)
Из (1) и (2) => ![]() ; (3)
; (3)
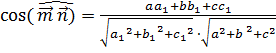 , где
, где![]() – угол между векторами m и n; (4)
– угол между векторами m и n; (4)
Подставляем (4) в (3) и т.к. ∠(a;b)= ∠(a;γ), то получаем:
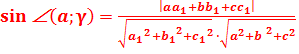
4. Если координаты вектора нормали неизвестны, то нам необходимо знать уравнение плоскости.
Любая плоскость в прямоугольной системе координат может быть задана уравнением
где хотя бы один из коэффициентов a, b, c отличен от нуля. Эти коэффициенты и будут координатами вектора нормали, т.е. ![]() {a; b; c}.
{a; b; c}.
Алгоритм решения задач на нахождение угла между прямой и плоскостью с помощью метода координат:
- Делаем рисунок, на котором отмечаем прямую и плоскость;
- Вводим прямоугольную систему координат ;
- Находим координаты направляющего вектора по координатам его начала и конца ;
- Находим координаты вектора нормали к плоскости;
- Подставляем полученные данные в формулу синуса угла между прямой и плоскостью;
- Находим значение самого угла.
Рассмотрим задачу:
1. В кубе ABCDA1B1C1D1 найдите тангенс угла между прямой AC1 и плоскостью BDD1 .
Решение:
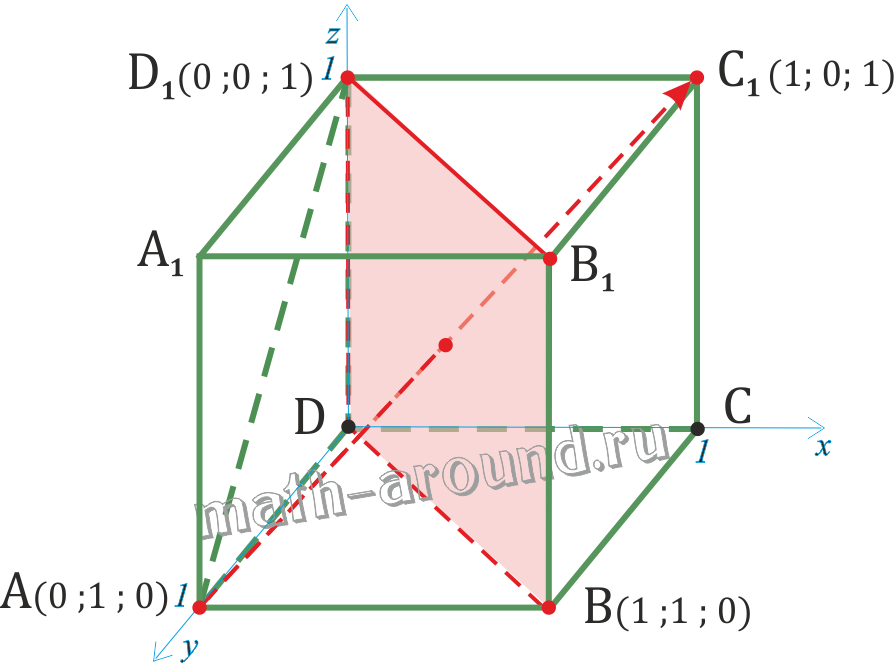
1. Введем прямоугольную систему координат с началом координат в точке D.
2. Найдем координаты направляющего вектора АС1. Для этого сначала определим координаты точек А и С1:
А(0; 1; 0);
С1(1; 0; 1).
![]() {1; -1; 1}.
{1; -1; 1}.
3. Найдем координаты вектора нормали к плоскости BB1D1. Для этого найдем координаты трех точек плоскости, не лежащих на одной прямой, и составим уравнение плоскости:
D(0; 0; 0);
D1(0; 0; 1);
В(1; 1; 0);
Уравнение плоскости имеет вид ax+by+cz+d=0. Подставим в это уравнение координаты точек:
D: a⋅0+b⋅0+c⋅0+d=0;
D1: a⋅0+b⋅0+c⋅1+d=0;
B: a⋅1+b⋅1+c⋅0+d=0.
Получили систему из трех уравнений:
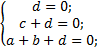
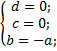
Подставим в уравнение: a⋅x+(-a)⋅y+0⋅z+0 = 0;
a⋅x-a⋅y = 0; |:a
x-y = 0.
Т.о., вектор нормали к плоскости BDD1 имеет координаты:
![]() {1;-1; 0}.
{1;-1; 0}.
4. Найдем синус между прямой АС1 и плоскостью BDD1:
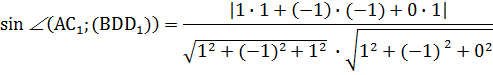
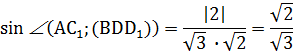
5. Воспользуемся основным тригонометрическим тождеством и найдем косинус угла между прямой АС1 и плоскостью BDD1:
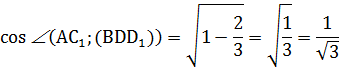
6. Найдем тангенс угла между прямой АС1 и плоскостью BDD1:
![]() ;
;
![]() .
.
Ответ: ![]() .
.
2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, найдите синус угла между прямой BD и плоскостью SBC.
Решение:
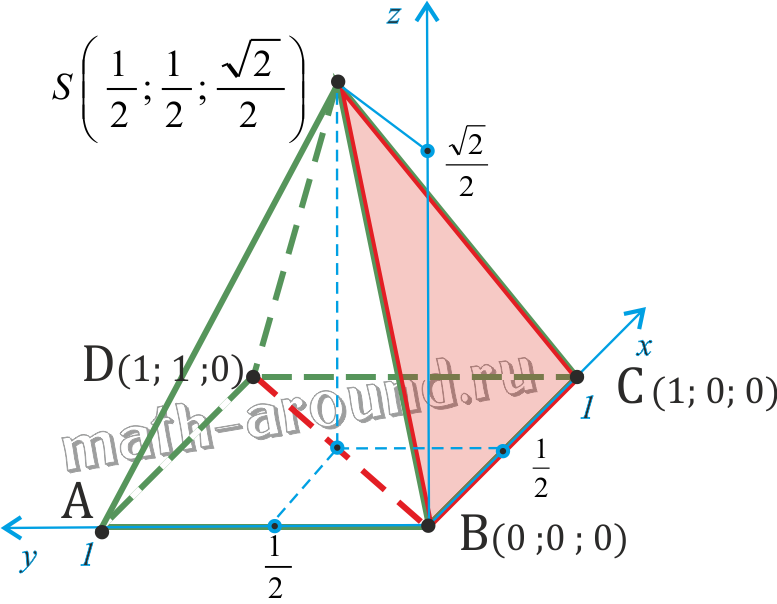
1. Введем прямоугольную систему координат с началом координат в точке B.
2. Найдем координаты направляющего вектора BD. Для этого сначала определим координаты точек B и D:
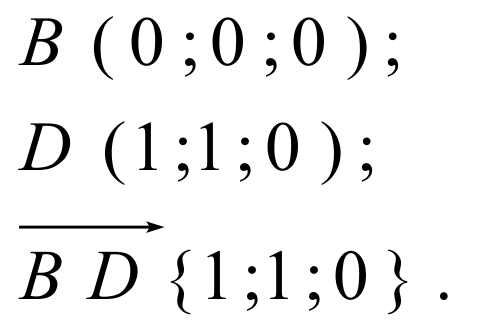
3. Найдем координаты вектора нормали к плоскости SBC. Для этого найдем координаты трех точек плоскости, не лежащих на одной прямой, и составим уравнение плоскости SBC:
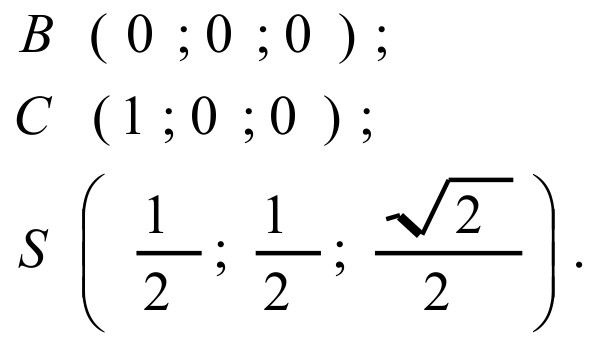
Как получили координаты точки S ?
Из точки S опустили перпендикуляр к плоскости основания ABC. Точку пересечения обозначили О. Точка О - проекция точки S на плоскость ABC. Ее координаты по осям х и у будут первыми двумя координатами точки S.
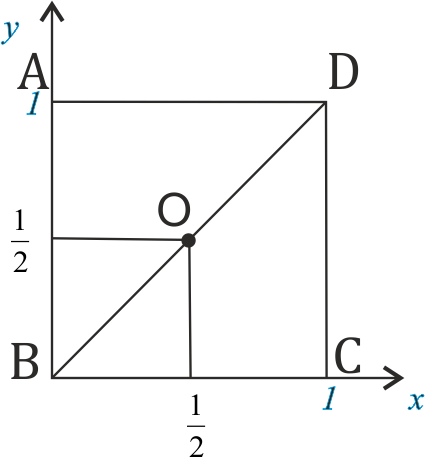
Узнав значение высоты пирамиды, мы нашли третью координату точки S (по оси z)
Треугольник SOB - прямоугольный, следовательно, по теореме Пифагора:
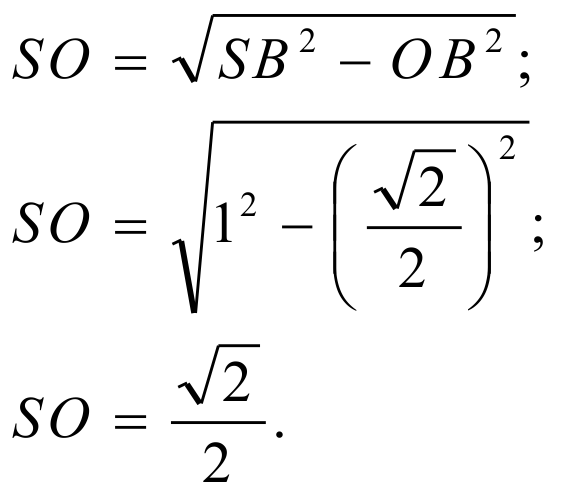
Уравнение плоскости имеет вид ax+by+cz+d=0. Подставим в это уравнение координаты точек:
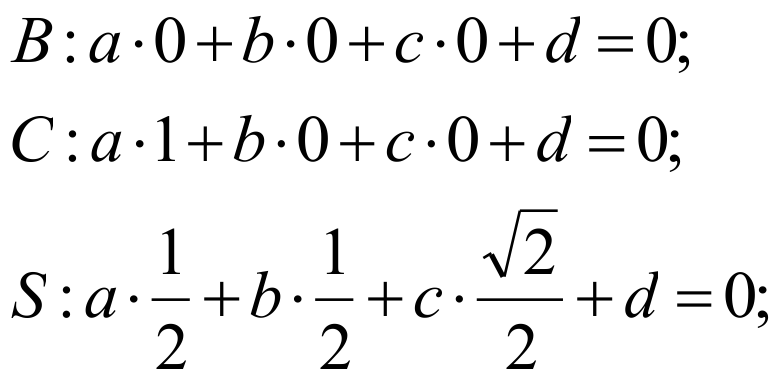
Получили систему из трех уравнений:
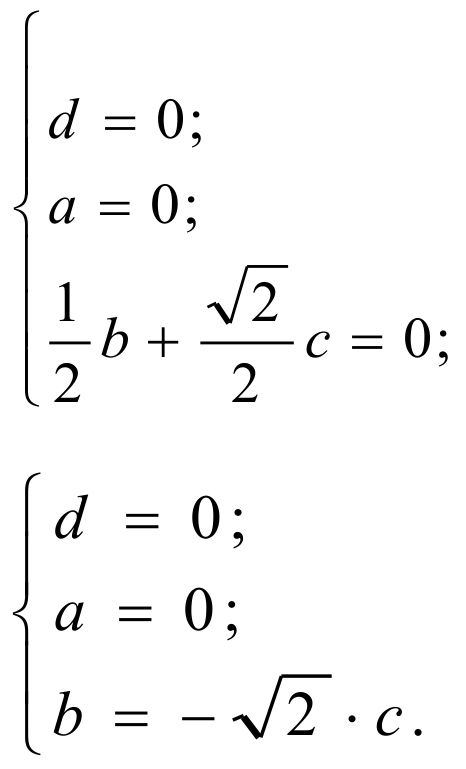
Подставим в уравнение:
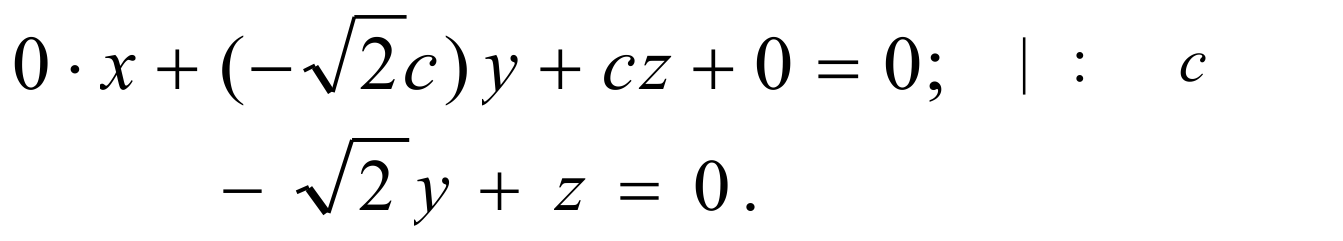
Т.о., вектор нормали к плоскости SBD имеет координаты:
![]() .
.
4. Найдем синус между прямой BD и плоскостью SBD:
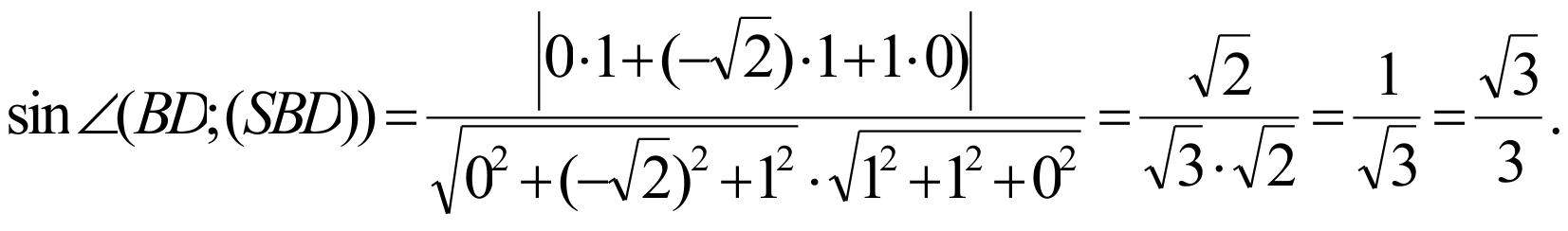
Ответ: ![]() .
.
- отправить денежный перевод с карты на карту мгновенно и без комиссий по ссылке . Ссылка на перевод . В поле «Добавьте комментарий» необходимо указать «в дар» или «подарок».
- оставить комментарий ниже.
Автор: Аникина Марина
Создан: 09.03.2014
Просмотр:44897
Комментарии к этой заметке:
Добавить Ваш комментарий
