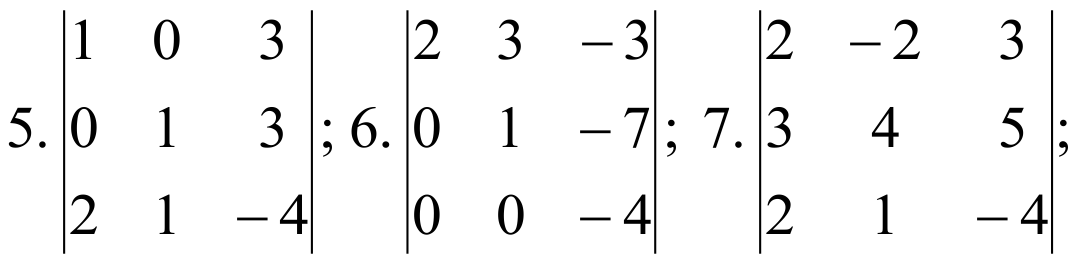
Определители
«Если Вы хотите научиться плавать, то смело входите в воду,
а если хотите научиться решать задачи,
то решайте их.»
Д. Пойа (1887-1985 г.)
(Математик. Внёс большой вклад в популяризацию математики. Написал несколько книг о том, как решают задачи и как надо учить решать задачи.)
Уважаемые студенты,
каждый месяц у вас есть возможность попасть на бесплатный вебинар по высшей математике. Темы предстоящих вебинаров выбираем все вместе в Телеграм-канале (ТК). Переходите, кликнув по иконке 
Там же будут ссылки на трансляции вебинаров за 30-60 минут до начала. Так что заходите в ТК.
Определители.
С каждой квадратной матрицей связывают число. Это число называется определителем матрицы. Определитель вычисляется по особым правилам и обозначается |A|, det A, ΔA.
Число строк (столбцов) определителя называется его порядком.
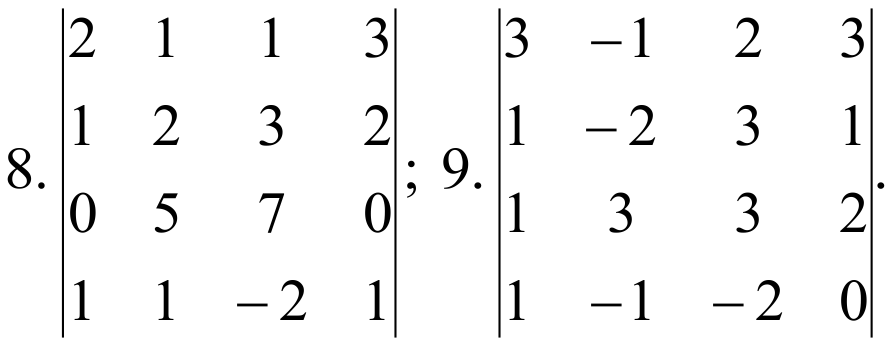
Определитель первого порядка матрицы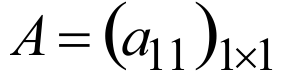 
равен элементу a11: |A|=a11
ПРИМЕРЫ:
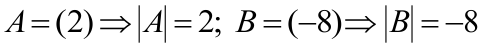
Не путать определитель первого порядка с модулем.
Определитель второго порядка обозначается символом
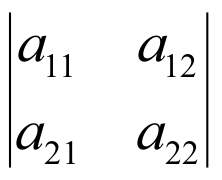
и равен
ПРИМЕРЫ:
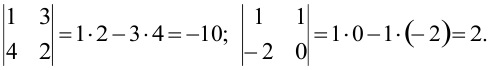
Определитель 3-го порядка обозначается символом
и равен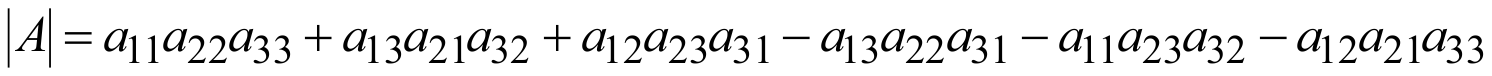 
Для запоминания этой формулы используют схематические правила (правило треугольника или Саррюса)
Правило Саррюса.
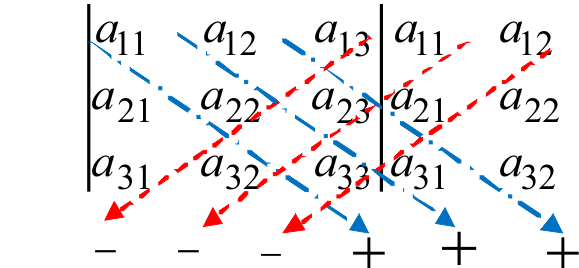
Правило треугольника.
Посмотрим на примере, как используются эти правила.
ПРИМЕР:
Правило Саррюса
Допишем к определителю два первых столбца.
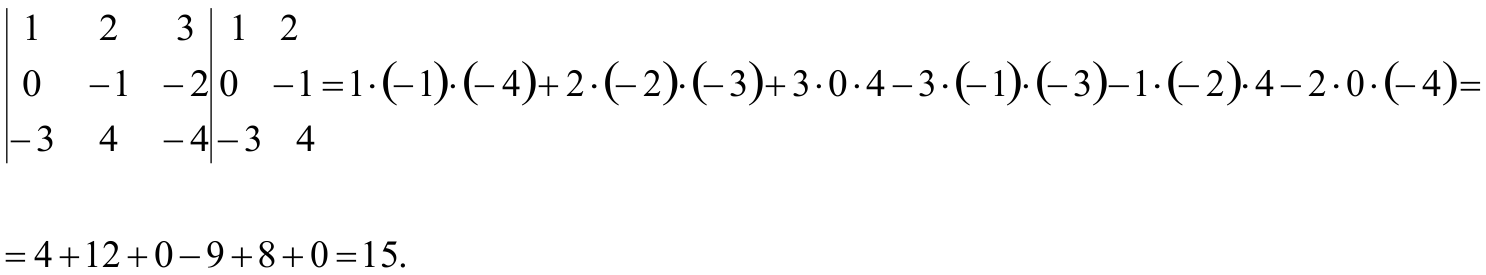
Правило треугольника
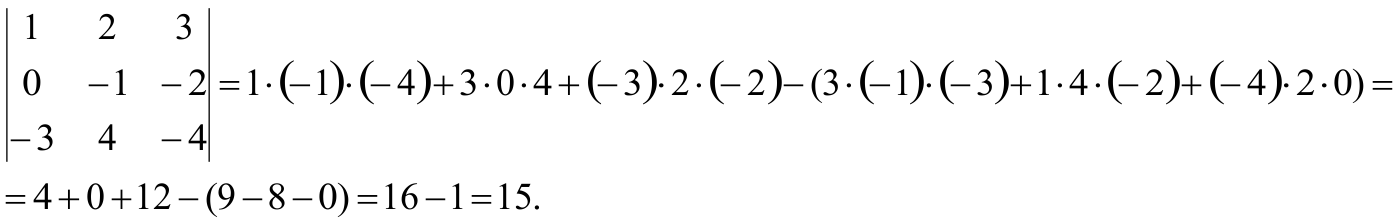
Такой способ вычисления определителей не подходит для определителей 4-го порядка и выше. Прежде чем указать правило, которое позволяет находить определители любого порядка, рассмотрим понятие алгебраического дополнения элемента матрицы.
Алгебраическим дополнением (Аij ) элемента аij определителя матрицы А называется число, равное произведению (-1)i+j (в степени номер строки плюс номер столбца этого элемента) на определитель, который получается из данного в результате вычеркивания строки и столбца, где стоит этот элемент.
ПРИМЕР:
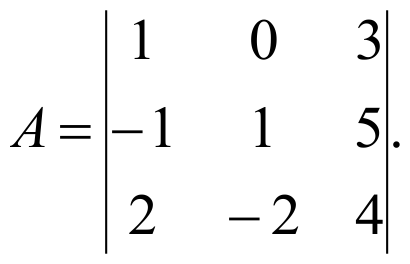
Вычислить алгебраическое дополнение А21 элемента а21 .
РЕШЕНИЕ:
По определению алгебраического дополнения
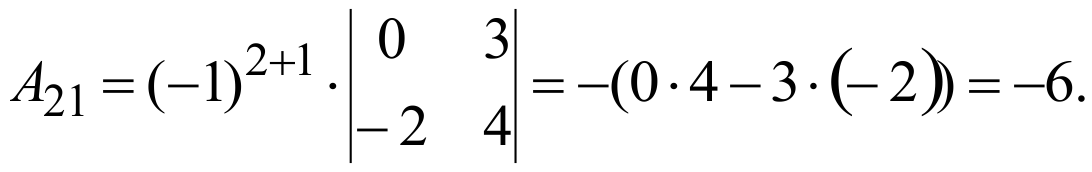
Вычисление определителя произвольного порядка.Определитель равен сумме произведений элементов любой его строки (или столбца) на соответствующие алгебраические дополнения.
Например, разложение определителя 4-го порядка по первой строке выглядит следующим образом: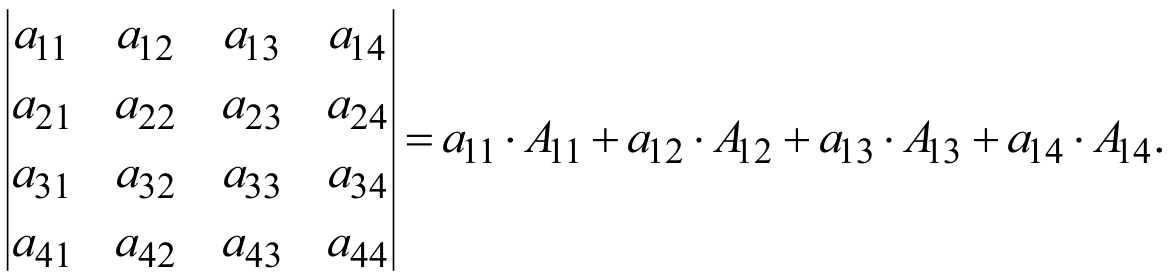
ПРИМЕР: Вычислить определитель
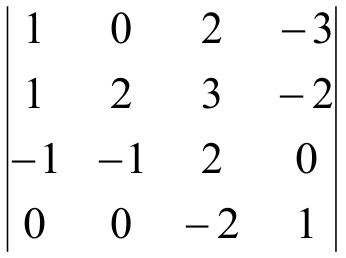
РЕШЕНИЕ: Разложим определитель по второму столбцу (Выбирать лучше ту строку (или тот столбец), где больше нулей, если они есть).
Если Вам понравился урок и появилось желание поддержать нас, Вы можете:
- отправить денежный перевод (комиссия за операцию 1%) по ссылке Ссылка на перевод.
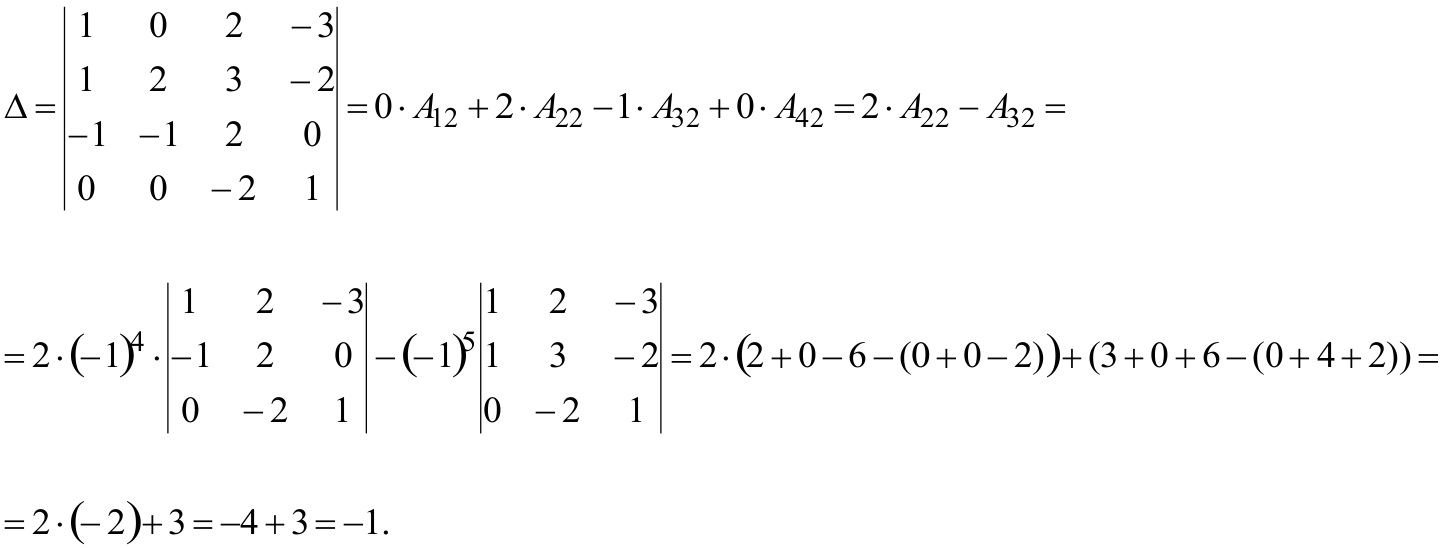
В открывшемся окне:
- поставить галочку возле «Добавить сообщение получателю»
- в появившемся поле оставить сообщение «в дар» или «подарок».
ИЛИ
- оставить комментарий ниже.
Упражнения к уроку:
Автор: Аникина Анна
Создан: 16.03.2014
Просмотр:45213
Комментарии к этой заметке:
Огромное спасибо !!! Творческих успехов вам !!!
Добавить Ваш комментарий
Семби
25.09.2020