Системы линейных уравнений
«Если Вы хотите научиться плавать, то смело входите в воду,
а если хотите научиться решать задачи,
то решайте их.»
Д. Пойа (1887-1985 г.)
(Математик. Внёс большой вклад в популяризацию математики. Написал несколько книг о том, как решают задачи и как надо учить решать задачи.)
Уважаемые студенты,
каждый месяц у вас есть возможность попасть на бесплатный вебинар по высшей математике. Темы предстоящих вебинаров выбираем все вместе в Телеграм-канале (ТК). Переходите, кликнув по иконкеТам же будут ссылки на трансляции вебинаров за 30-60 минут до начала. Так что заходите в ТК.
Системы линейных уравнений.
Система уравнений вида
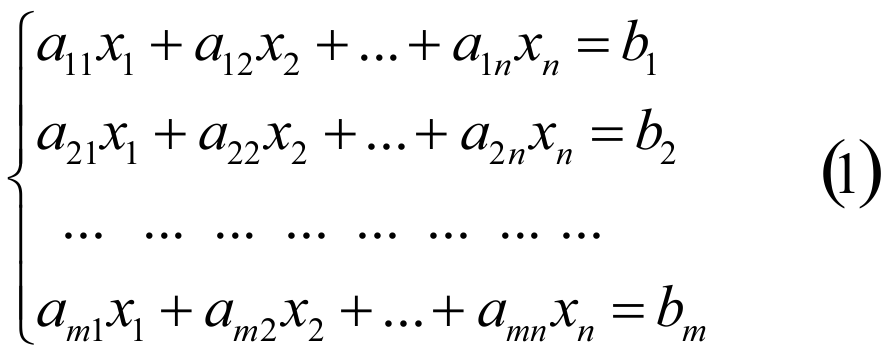
называется системой m линейных уравнений с n неизвестными, где x1, x2,...,xn - неизвестные; aij - коэффициенты при неизвестных; b1, b2,...,bm - свободные члены.
Решением СЛУ называется упорядоченный набор чисел {c1, c2,..., cn} такой, что при подстановке его в каждое уравнение системы получаем верное числовое равенство.
Если система имеет хотя бы одно решение, то она называется совместной, в противном случае несовместной.
Совместная система называется определенной, если она имеет единственное решение.
Если совместная система имеет более одного решения, то она называется неопределенной.
Если b1= b2=...=bm=0, то СЛУ (1) называется однородной.
Матрица
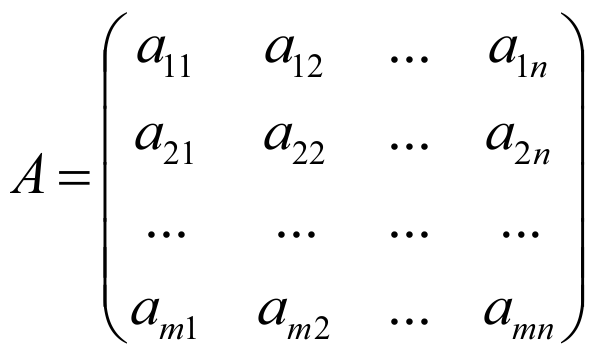
(матрица, составленная из коэффициентов при неизвестных) называется матрицей системы (или матрицей коэффициентов).
Матрица
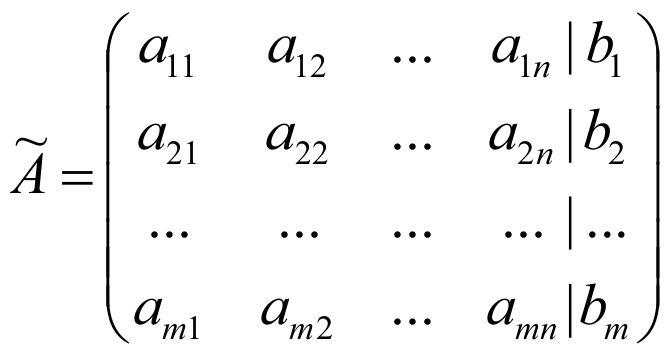
(матрица, составленная из коэффициентов при неизвестных и столбца свободных членов) называется расширенной матрицей системы.
- отправить денежный перевод (комиссия за операцию 1%) по ссылке Ссылка на перевод.
В открывшемся окне:
- поставить галочку возле «Добавить сообщение получателю»
- в появившемся поле оставить сообщение «в дар» или «подарок».
ИЛИ
- оставить комментарий ниже.
Автор: Аникина Анна
Создан: 28.03.2014
Просмотр:44896
Комментарии к этой заметке:
Добавить Ваш комментарий
