Найти ранг матрицы:
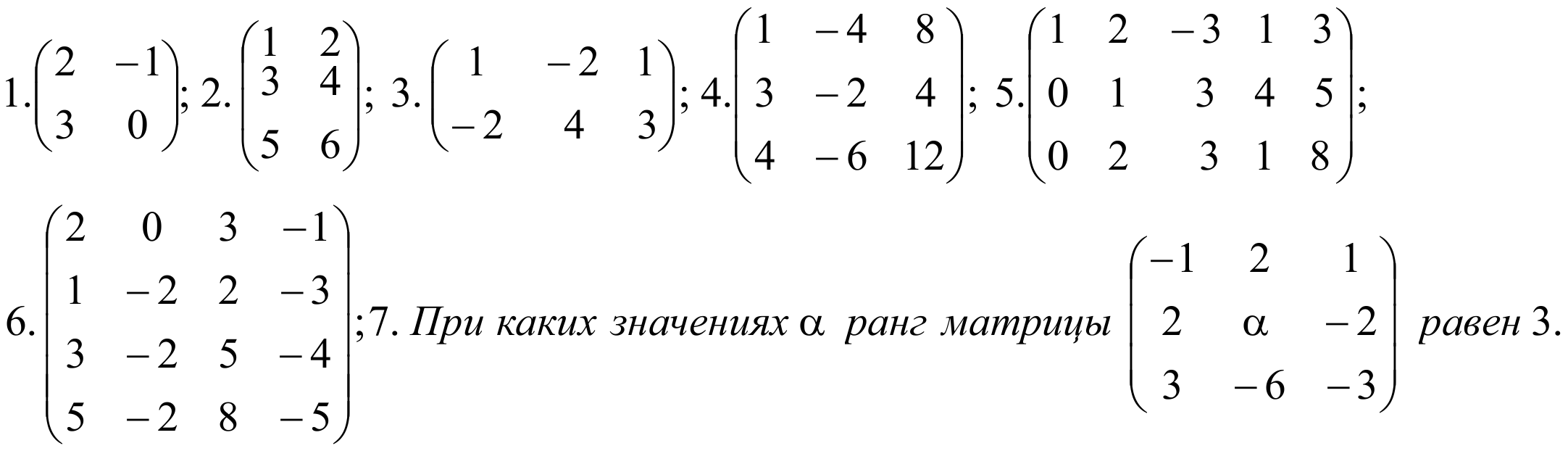

Ранг матрицы. Элементарные преобразования строк матрицы.
«Если Вы хотите научиться плавать, то смело входите в воду,
а если хотите научиться решать задачи,
то решайте их.»
Д. Пойа (1887-1985 г.)
(Математик. Внёс большой вклад в популяризацию математики. Написал несколько книг о том, как решают задачи и как надо учить решать задачи.)
Там же будут ссылки на трансляции вебинаров за 30-60 минут до начала. Так что заходите в ТК.
Рассмотрим матрицу
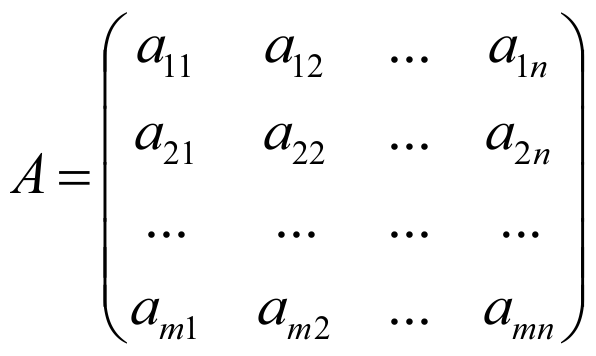 .
.
Выделим в ней k-строк и k-столбцов (k≤(min(m,n))). Из элементов, стоящих на пересечении выделенных строк и столбцов, составим определитель k-го порядка. Все такие определители называются минорами этой матрицы.
Рассмотрим всевозможные миноры матрицы А, отличные от нуля.
Рангом матрицы А называется наибольший порядок минора этой матрицы, отличного от нуля.
Если все элементы матрицы равны нулю, то ранг этой матрицы принимают равным нулю.
Минор, порядок которого определяет ранг матрицы, называется базисным.
У матрицы может быть несколько базисных миноров.
Ранг матрицы А обозначается r(A) . Если r(A)=r(B) , то матрицы А и В называются эквивалентными. Пишут A̴∼В.
Свойства ранга матрицы:
Под элементарными преобразованиями понимают:
При вычислении ранга матрицы могут быть использованы элементарные преобразования, метод приведения матрицы к ступенчатому виду, метод окаймляющих миноров.
Метод приведения матрицы к ступенчатому виду заключается в том, что при помощи элементарных преобразований данная матрица приводится к ступенчатой.
Матрица называется ступенчатой, если в каждой ее строке первый ненулевой элемент стоит правее, чем в предыдущей (т. е. получаются ступеньки, высота каждой ступеньки должна быть равна единице).
Примеры ступенчатых матриц:
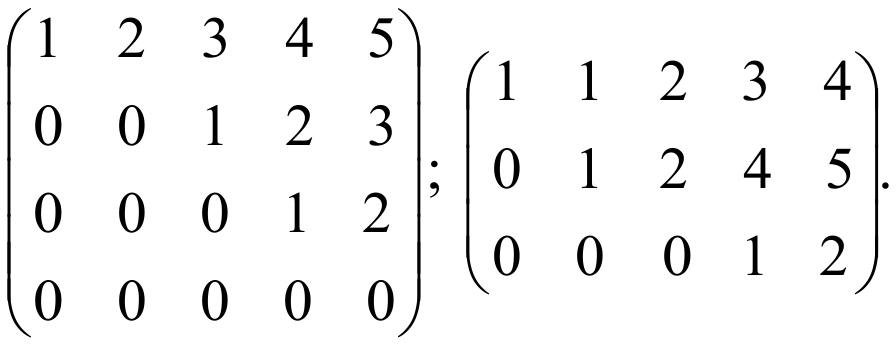
Примеры не ступенчатых матриц:
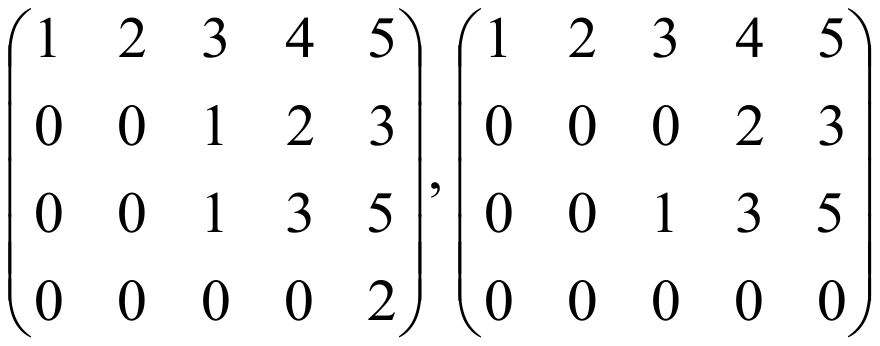
ПРИМЕР: Найти ранг матрицы:
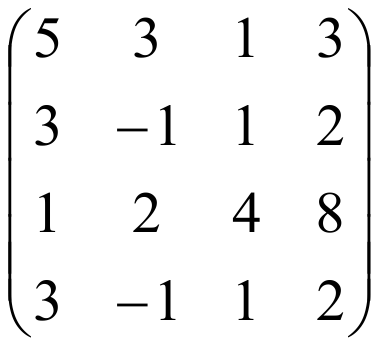
РЕШЕНИЕ:
Приведем данную матрицу к ступенчатой с помощью элементарных преобразований.
1.Поменяем местами первую и третью строки.

2. Получим в первом столбце нули под единицей.
Прибавив ко второй строке первую, умноженную на (-3), к третьей – первую, умноженную на (-5), к четвертой – первую, умноженную на (-3), получим
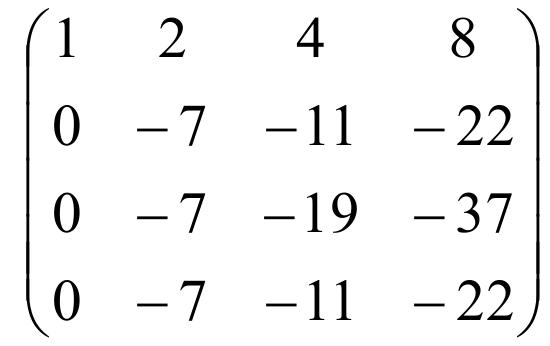
Для того чтобы было понятней где еще нужно получить нули, нарисуем ступеньки в матрице. (Матрица будет ступенчатой, если везде под ступеньками будут нули)
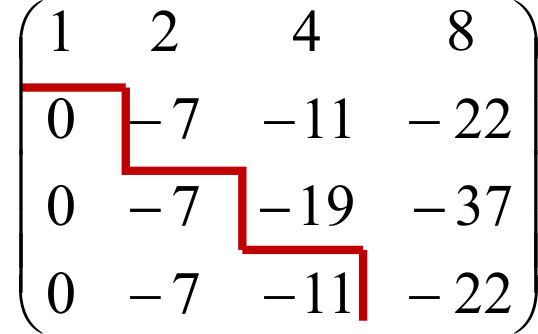
3. Прибавив к третьей строке вторую, умноженную на (-1), к четвертой – вторую, умноженную на (-1), получим нули под ступеньками во втором столбце.
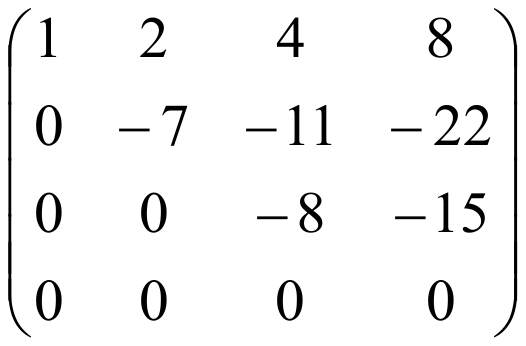
Если нарисовать опять ступеньки, увидим, что матрица ступенчатая.

Ее ранг равен r=3 (число строк ступенчатой матрицы, в каждой из которых хотя бы один элемент отличен от нуля). Следовательно, ранг данной матрицы r=3.
Решение можно записать так:

(римскими цифрами обозначены номера строк)
Ответ: r=3.
Минор порядка k+1, содержащий в себе минор порядка k называется окаймляющим минор.
Метод окаймляющих миноров основан на том, что ранг данной матрицы равен порядку такого минора этой матрицы, который отличен от нуля, а все окаймляющие его миноры равны нулю.
ПРИМЕР : Найти ранг матрицы:
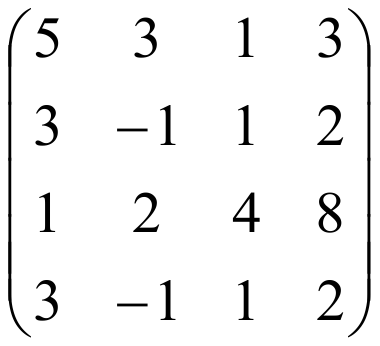
РЕШЕНИЕ:
Найдем теперь ранг этой матрицы методом окаймляющих миноров.
Среди миноров первого порядка есть отличные от нуля, например 5. Среди окаймляющих его миноров есть отличный от нуля, например
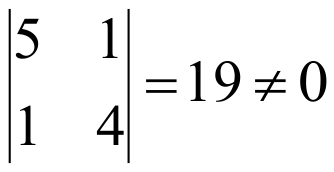
Среди миноров, окаймляющих этот минор, есть отличный от нуля, например
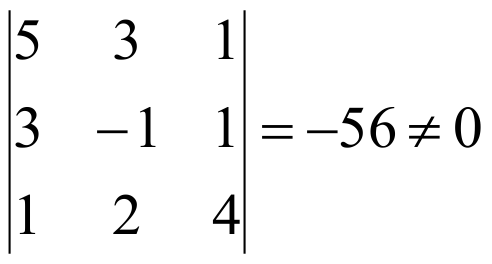
Так как единственный минор, окаймляющий последний минор равен нулю, то r=3.
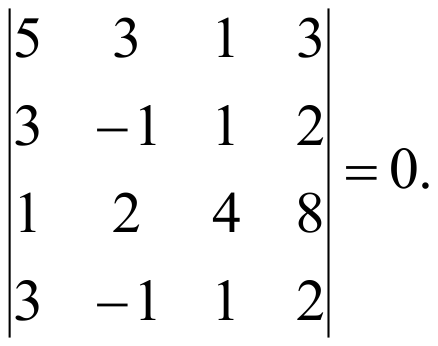
Ответ: r=3.
В открывшемся окне:
Найти ранг матрицы:
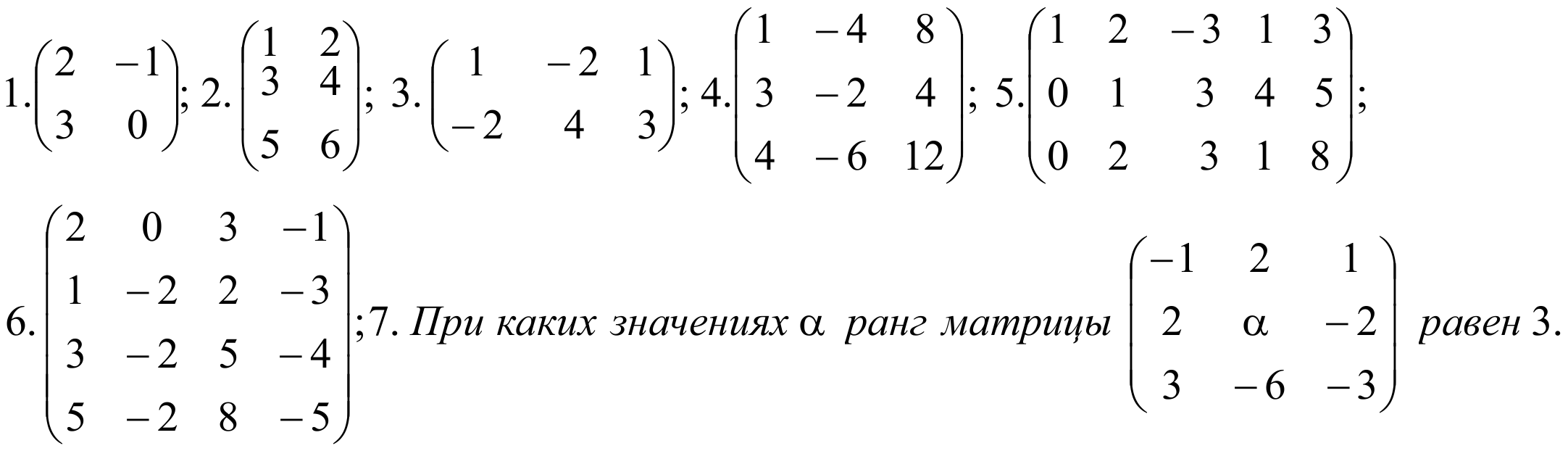
Автор: Аникина Анна
Создан: 25.09.2014
Просмотр:62170
Комментарии к этой заметке:
Добавить Ваш комментарий