Решите системы методом Гаусса
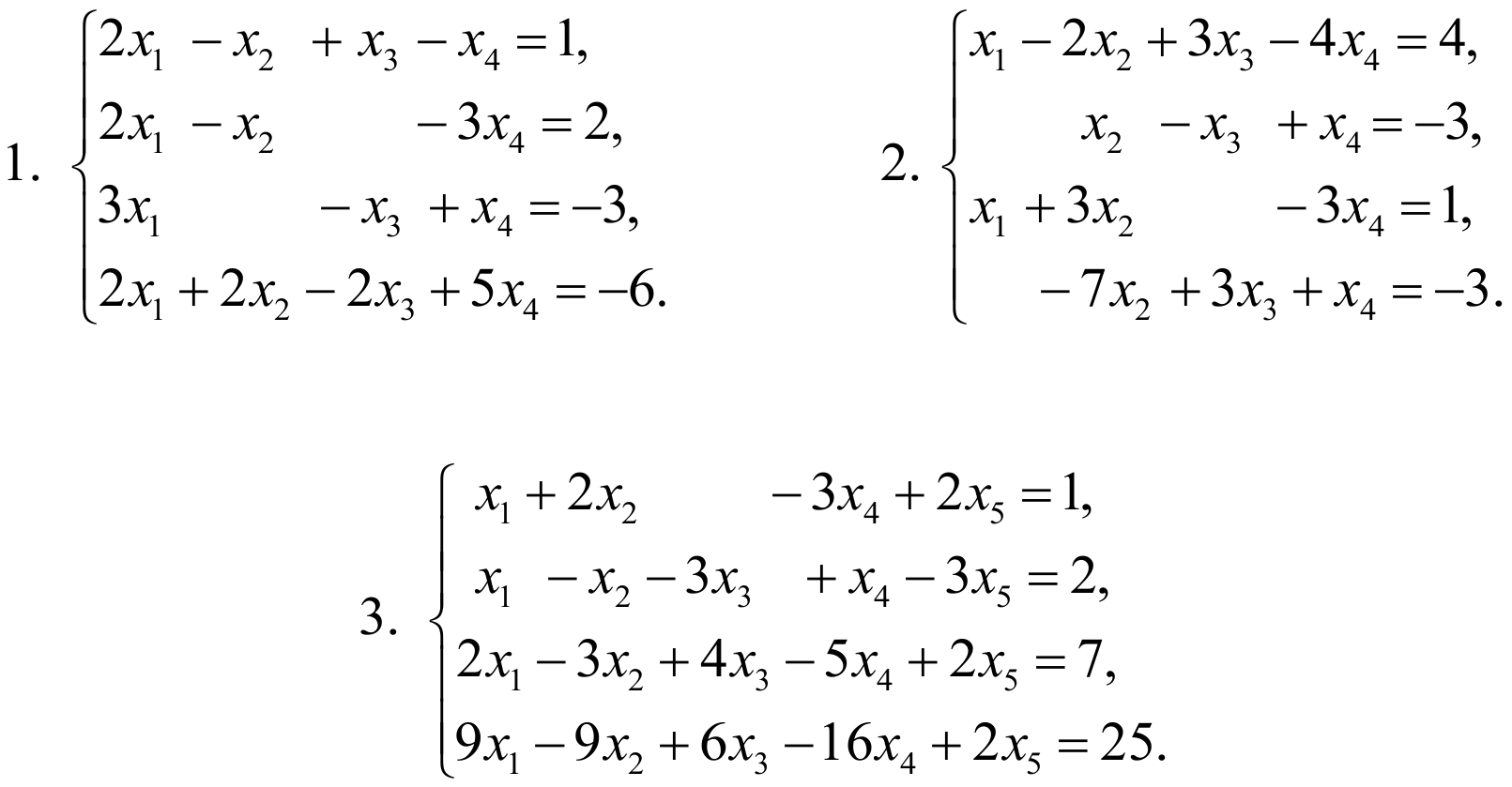

Теорема Кронекера-Капелли. Метод Гаусса.
«Если Вы хотите научиться плавать, то смело входите в воду,
а если хотите научиться решать задачи,
то решайте их.»
Д. Пойа (1887-1985 г.)
(Математик. Внёс большой вклад в популяризацию математики. Написал несколько книг о том, как решают задачи и как надо учить решать задачи.)
Там же будут ссылки на трансляции вебинаров за 30-60 минут до начала. Так что заходите в ТК.
Пусть дана система m линейных уравнений с n неизвестными
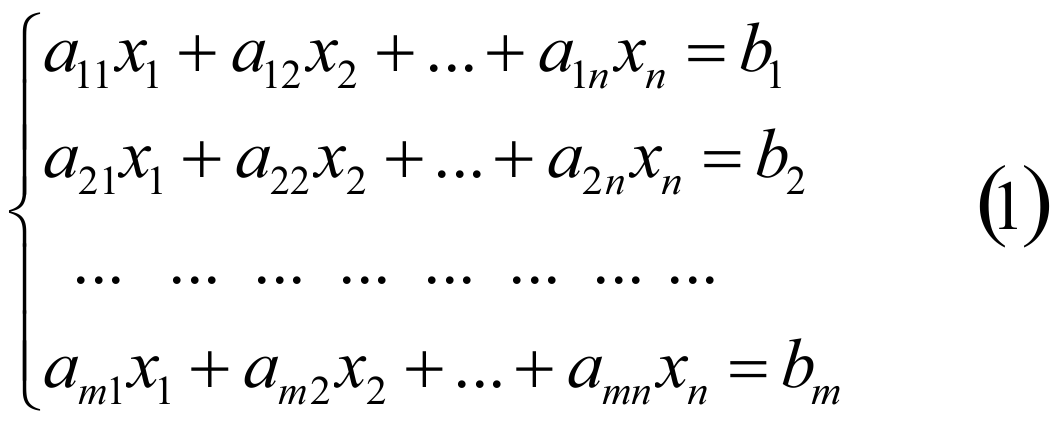 .
.
На вопрос о совместности этой системы дает теорема Кронекера-Капелли.
Какая система называется совместной читать здесь
Теорема Кронекера-Капелли: Система линейных уравнений (СЛУ) совместна тогда и только тогда, когда ранг расширенной матрицы системы (rp) равен рангу основной матрицы (ro).
Что называется расширенной матрицей читать здесь
Что такое ранг матрицы и как его найти читать здесь
Правила отыскания всех решений совместной системы линейных уравнений вытекают из следующих теорем.
Теорема 1: Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение.
Теорема 2: Если ранг совместной системы меньше числа неизвестных, то система имеет бесконечно много решений.
МЕТОД ГАУССА
Одним из наиболее универсальных и эффективных методов решения СЛУ является МЕТОД ГАУССА, состоящий в последовательном исключении неизвестных.
СУЩНОСТЬ МЕТОДА ГАУССА. Расширенную матрицу системы с помощью элементарных преобразований приводят к ступенчатой, восстанавливают систему, которая является равносильной исходной системе, и находят решение.
Как данную матрицу привести к ступенчатой читать здесь
Рассмотрим этот метод на примерах.
ПРИМЕР 1:
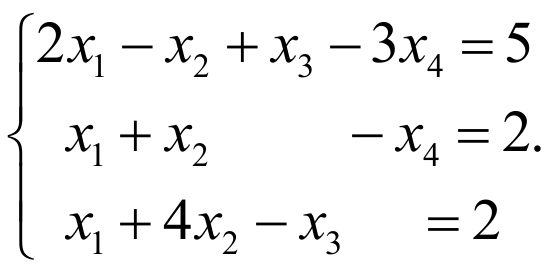
РЕШЕНИЕ:
Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду.
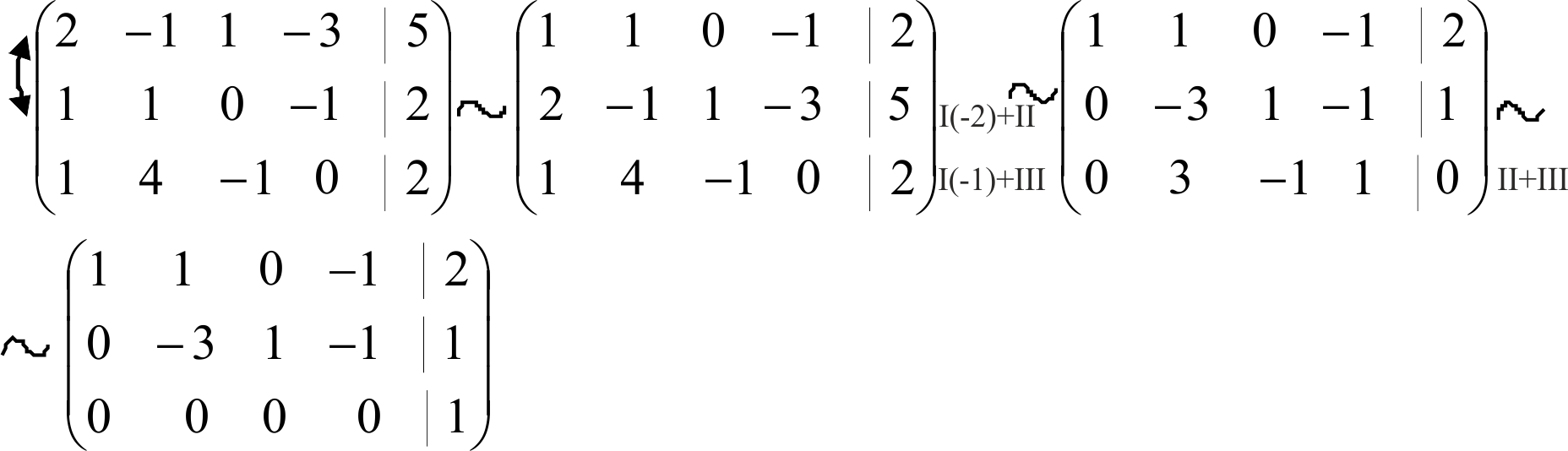
Ранг основной матрицы равен 2 (ro=2), а ранг расширенной – 3 (rp=3), поэтому по теореме Кронекера-Капелли система несовместна.
(Последняя строка представляет собой уравнение вида: 0=1. Поэтому делаем вывод, что система несовместна.)
Ответ: система несовместна.
Замечание: Если хотя бы одна строка имеет вид:
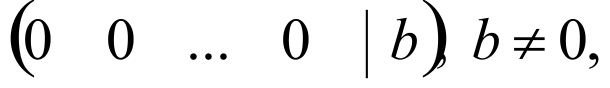
ПРИМЕР 2:
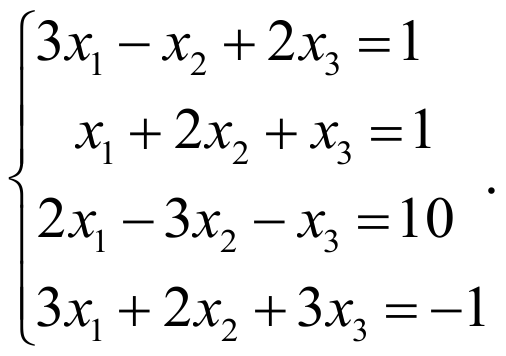
РЕШЕНИЕ:

ro=rp=3, поэтому по теореме Кронекера-Капелли система совместна, причем ранг системы равен числу неизвестных, следовательно система имеет единственное решение.
Найдем его
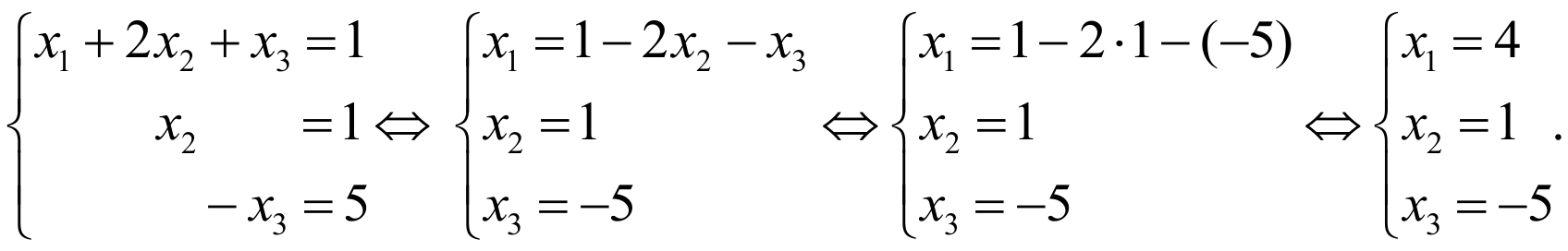
Ответ: (4;1;-5)
ПРИМЕР 3:
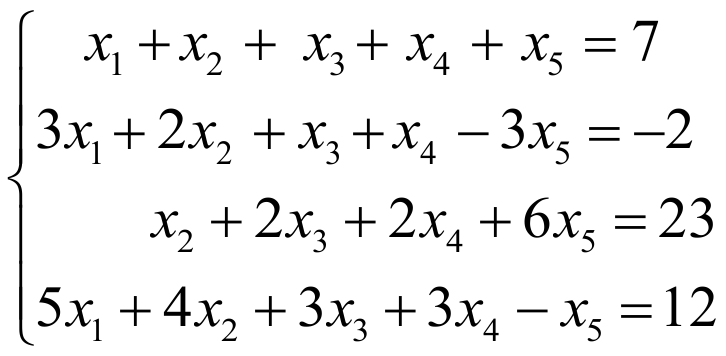
РЕШЕНИЕ:

Третья и четвертая строки получились нулевыми. Их можно вычеркнуть.
ro=rp=2, поэтому по теореме Кронекера-Капелли система совместна, причем ранг системы меньше числа неизвестных, следовательно система имеет бесконечное число решений.
Найдем их
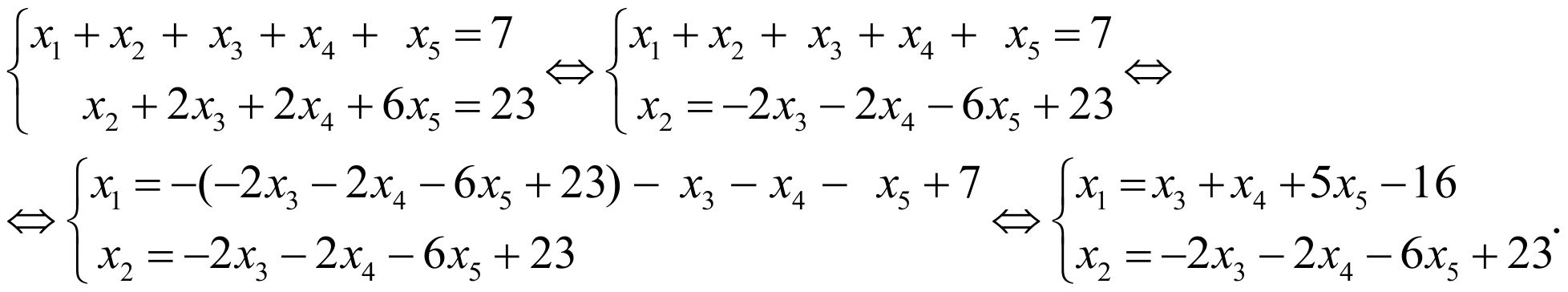
Ответ:
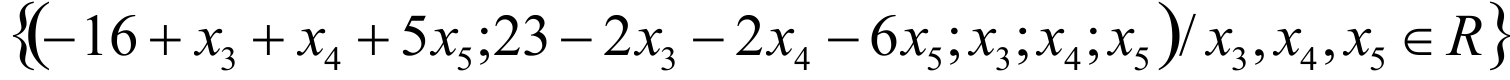
В открывшемся окне:
Решите системы методом Гаусса
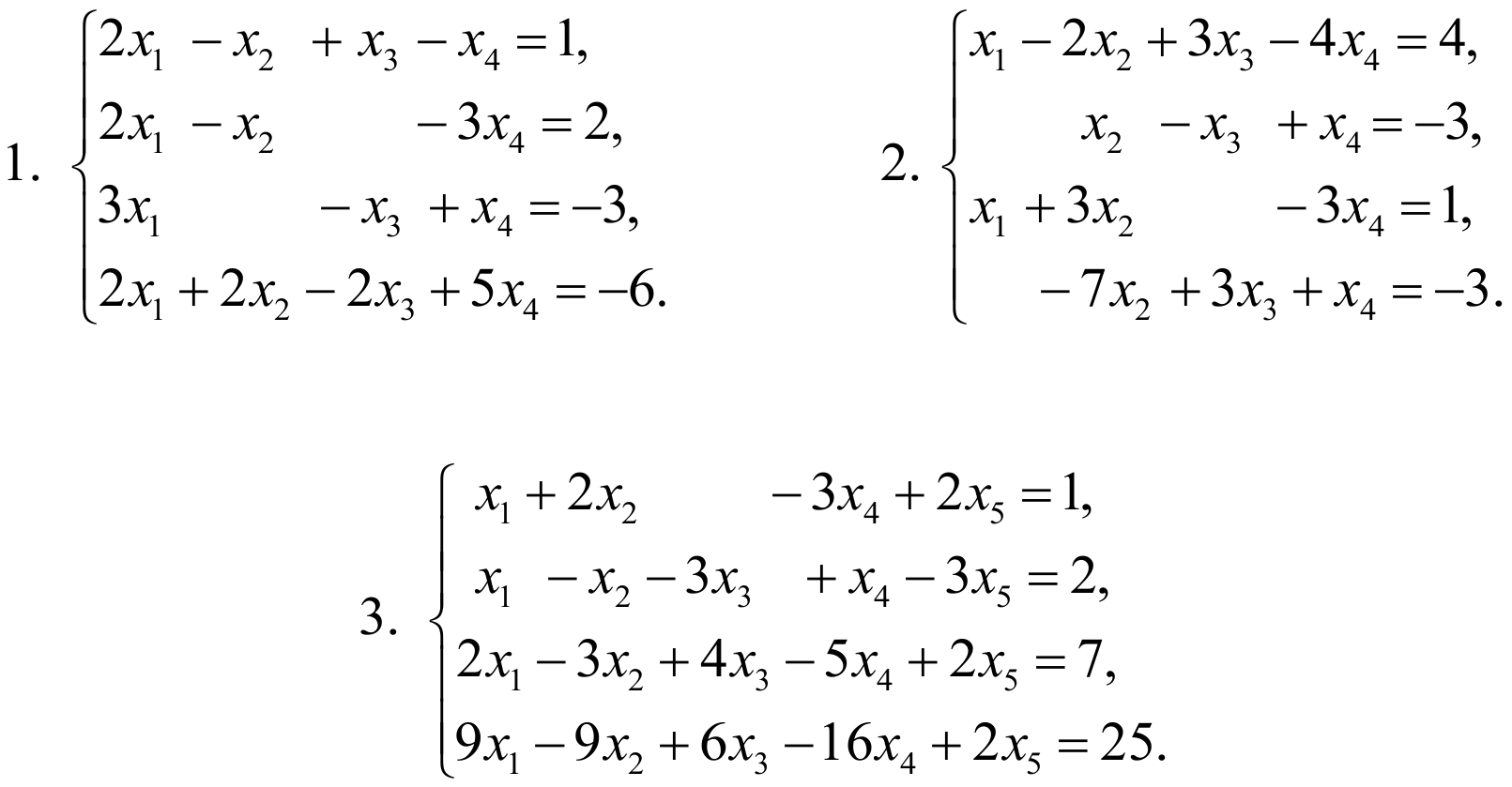
Автор: Аникина Анна
Создан: 25.09.2014
Просмотр:62607
Комментарии к этой заметке:
Добавить Ваш комментарий