В теории вероятности мы имеем дело с  экспериментами и опытами, которые проводятся в одинаковых условиях несколько раз.
Под опытом (экспериментом, испытанием) понимается осуществление  определенного (неизменяемого) комплекса условий.
В результате каждого эксперимента наблюдаем исход.
Этот исход может быть случаен (не предсказуем).
Одним из основных понятий теории вероятности является случайное событие и появляется оно в результате выполнения опыта.
Определение. Случайное событие (далее -  «событие» )– событие, которое может наступить в ходе некоторого опыта, а может не наступить.
Обозначение: А,B,C,….  (обозначаются заглавными латинскими буквами, за исключением  буквы P); А₁, А₂, А₃, ... (заглавными латинскими буквами с нижним индексом) 

1. Выпадение  4 очков при бросании игрального кубика один раз (опыт-бросание кубика 1 раз; событие – выпадение 4 очков).
2. Выпадение 3 орлов при бросании монеты 4 раз (опыт – бросание монеты 4 раза; событие – выпадение 3 орлов).
3. Появление брака при выборе одного изделия (опыт – выбор изделия 1 раз; событие – бракованное изделие).

ВИДЫ СОБЫТИЙ

Достоверным называется событие, которое обязательно произойдет в результате каждого опыта.
Обозначение: Ω.
Пример: Проводится опыт, в котором подбрасывают монету один раз. А – событие, в результате которого выпадет или орел, или решка. При подбрасывании монеты возможно 2 исхода: выпадет орёл, выпадет решка. Получается, что событие А произойдет всегда.
Невозможным называется событие, которое не может произойти в результате опыта.
Обозначение:Ø
Примеры:

• Проводят опыт, в котором из колоды карт (количество карт 36: от 6 до туза, всех мастей)выбирают одну карту. А – событие, в  котором выбрали карту с цифрой 2. Получается, что событие А никогда не произойдет, т.к. в колоде нет карт с такой цифрой.
• Проводят опыт, в котором игральный кубик бросают 2 раза и находят сумму очков . А- событие, в котором мы должны получить в результате 20 очков. Это невозможно, т.к. максимальное выпадение очков при каждом бросании кубика – 6, т.е. наибольшая  сумма, которая возможна -  12.

Несовместными называются события, которые в одном опыте не могут произойти одновременно (вместе). В противном случае они называются совместными.
Пример несовместных событий:

• Проводят опыт, в котором монету бросают 1 раз. Событие А- выпадет решка. Событие В- выпадет орел. При подбрасывании монеты возможно 2 исхода: выпадет орёл, выпадет решка. Получается, что в результате опыта события А, В одновременно произойти не могут. Т.о., А и В – несовместны.

противоположным событием

ОПЕРАЦИИ НАД СОБЫТИЯМИ

1. СУММА ( ОБЪЕДИНЕНИЕ).
   Определение: Суммой(объединением) событий А и В называется событие, которое состоит в том, что происходит хотя бы одно из событий (т.е. наступит или событие А, или событие В,  или оба события одновременно. Если события А и В несовместны, последний вариант отпадает, т.е. может наступить или событие А, или событие В ).
   Обозначение: А+В (или A U B).
   Примеры:
   • Проводят опыт, в котором монету бросают 2 раз. Событие А- выпадет орел при первом броске. Событие В- выпадет орел при втором броске. С = А + В-событие, в котором  хотя бы один раз выпадет орел (т.к. А и В совместны, то происходит или А, или В, или А ,В одновременно).

2. ПРОИЗВЕДЕНИЕ (ПЕРЕСЕЧЕНИЕ).

   Определение: Произведением (пересечением) событий А и В называется событие, которое состоит в том, что происходит и событие А, и событие В (одновременно).
   Обозначение: А•В (или ).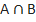
   Примеры:

   • Проводят опыт, в котором монету бросают 2 раз.
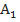     - выпадет орел при первом броске;
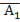      - выпадет решка при первом броске;
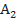     - выпадет орел при втором броске;
      - выпадет решка при втором броске;

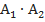    – событие, в котором орел выпадет при  двух  бросках.
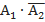    – событие, в котором при первом броске выпадет орел, а при втором решка.
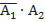    - событие, в котором при первом броске выпадет решка, а при втором орел.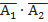– событие, в котором решка выпадет при двух бросках.

ТЕОРЕМЫ

1. ТЕОРЕМЫ СЛОЖЕНИЯ ВЕРОЯТНОСТЕЙ.
а) Вероятность сложения произвольных событий А и В равна сумме их вероятностей за вычетом вероятности произведения событий:

P(A+B) = P(A) + P(B) - P(A•B)

б)Частный случай а.
Для несовместных событий  А и В         P(A•B) = 0     ,    поэтому   

P(A+B) = P(A) + P(B) .

2. ТЕОРЕМА ПРОИЗВЕДЕНИЯ ВЕРОЯТНОСТЕЙ:
а)Если события А и В независимы, то выполняется равенство  P(A•B) = P(A) • P(B).
б) Если выполняется равенство P(A•B) = P(A) • P(B), то  события А и В независимы.